视觉SLAM十四讲笔记

##　初识SLAM

flowchart LR
    sensor(传感器数据)
    frontEnd(前端视觉里程计)
    backEnd(后端非线性优化)
    mapping(建图)
    loopClosing(回环检测)
    sensor-->frontEnd-->backEnd-->mapping
    sensor-->loopClosing-->backEnd

步骤：

传感器数据读取
视觉里程计（Visual Odometry, VO）。估计相邻图像间相机的运动，以及局部地图的样子。主要用到图像特征提取和匹配
后端优化（Optimization）。接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化，得到全局一致的轨迹和地图。需要消除噪声问题，用到滤波和非线性优化算法
回环检测（Loop Closing）。判断机器人是否打到过先前位置，检测到回环提交给后端处理。SLAM时会出现累计误差需要回环检测消除
建图（Mapping）。根据估计的轨迹，建立任务对应的地图

VIO：视觉惯性里程计，视觉里程计+IMU

数学问题表述

用\(x\)表示机器人位置，离散时刻位置记为\(x_1,\ldots,x_k\)，构成轨迹，每个时刻传感器会测量到一部分路标点一共有N个，用\(y_1,\ldots,y_N\)表示

运动：考察从\(k-1\)时刻到\(k\)时刻，机器人的位置\(x\)的变化
观测：描述机器人在\(k\)时刻处于\(x_k\)位置处探测到了路标\(y_i\)

运动方程：

\[ x_k=f(x_{k-1},u_k,w_k) \]

\(u_k\)为运动传感器读数或者输出，\(w_k\)为噪声

观测方程：

\[ z_{k,j}=h(y_j,x_k,v_{k,j}) \]

机器人在\(x_k\)位置看到路标\(y_j\)产生了观测数据\(z_{k,j}\)，\(v_{k,j}\)为噪声

三维空间刚体运动

矩阵变换

欧式变换

\[ \left [ e_1,e_2,e_3 \right ]\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \left [ e_1' ,e_2',e_3' \right ]\begin{bmatrix} a_1' \\ a_2' \\ a_3' \end{bmatrix} \]

不同坐标系下向量\(a\)的坐标，两边乘\(\begin{bmatrix} {e_1}^{T} \\ {e_2}^{T} \\ {e_3}^{T} \end{bmatrix}\)可得到

\[ \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} e_1^T e_1^′ & e_1^T e_2^′ & e_1^T e_3^′ \\ e_2^T e_1^′ & e_2^T e_2^′ & e_2^T e_3^′ \\ e_3^T e_1^′ & e_3^T e_2^′ & e_3^T e_3^′ \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \triangleq Ra' \]

矩阵\(R\)为旋转矩\(\Leftrightarrow\)阵行列式为1的正交矩阵，定义

\[ \mathrm{SO}(n)=\left \{\boldsymbol{R}\in \mathbb{R}^{n\times n}|\boldsymbol{RR}^T=I,\det(\boldsymbol{R})=1\right \} \]

\[ \boldsymbol R^{-1}a=\boldsymbol R^Ta \]

特殊正交群(Special Orthogonal Group)

加上平移向量

\[ \boldsymbol{a'= Ra+ t} \]

变换

\[ \boldsymbol{b= R_1a+ t_1,\space c= R_2b+ t_2} \]

a到c变换为

\[ \boldsymbol{c=R_2( R_1a+ t_1)+ t_2} \]

变换后会很不方便，使用齐次坐标和变换矩阵

\[ \begin{bmatrix} \boldsymbol a' \\ 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol {R} & \boldsymbol{t} \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} \boldsymbol a \\ 1 \end{bmatrix} \triangleq \boldsymbol{T} \begin{bmatrix} \boldsymbol a \\ 1 \end{bmatrix} \]

\(\boldsymbol T\)为变换矩阵

\[ \mathrm{SE}(3)= \left \{T= \begin{bmatrix} R & t\\ 0^T & 1 \end{bmatrix} \in \mathbb{R}^{4\times 4} | R \in \mathrm{SO}(3), t\in \mathbb{R}^3 \right \} \]

\[ T^{-1}=\begin{bmatrix} R^T & -R^Tt\\ 0^T & 1 \end{bmatrix} \]

特殊欧氏群(Special Euclidean Group)

Eigen库

旋转向量和欧拉角

矩阵冗余

旋转轴用单位向量\(n\)表示，角度用\(\theta\)表示

和矩阵变换的关系：罗德里格斯公式（Rodrigues’s Formula）

\[ \boldsymbol R=\cos \theta \boldsymbol I + (1-\cos \theta)\boldsymbol n\boldsymbol n^T+\sin \theta \boldsymbol n^\wedge \]

\(n^\wedge\)是向量到反对称矩阵的转换符

\[ \boldsymbol a\times \boldsymbol b= \begin{Vmatrix} e_1 & e_2 & e_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{Vmatrix} = \begin{bmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{bmatrix} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \boldsymbol b \triangleq \boldsymbol a^\wedge \boldsymbol b \]

\[ \boldsymbol a^\wedge = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \]

罗德里格斯公式两边取迹（矩阵对角线元素之和）

\[ \begin{align*} \mathrm{tr}(\boldsymbol R)= & \cos\theta \space\mathrm{tr}(\boldsymbol I) + (1-\cos\theta)\space \mathrm{tr}(\boldsymbol n \boldsymbol n^T)+\sin\theta \space \mathrm{tr}(\boldsymbol n^\wedge) \\ \space = & 3\cos\theta + (1-\cos\theta)\\ = & 1+2\cos\theta \end{align*} \]

转轴\(n\)旋转\(n\)方向的向量结果不变

\[ \boldsymbol R\boldsymbol n= \boldsymbol n \]

转轴\(\boldsymbol n\)是矩阵\(\boldsymbol R\)特征值1对应的特征向量，求解方程归一化得到\(\boldsymbol n\)

欧拉角

yaw：偏航角，物体绕z轴旋转
pitch：俯仰角，绕y轴旋转的
roll：滚转角，绕x轴旋转

欧拉角的转动是按轴顺序来的

RPY角（xyz顺序）和Euler角（zyx）

万向锁

四元数

旋转矩阵冗余，欧拉角和旋转向量紧凑但是有奇异性

四元数有一个实部三个虚部

\[ q=q_0+q_1i+q_2j+q_3k \]

满足

\[ \begin{cases} i^2=j^2=k^2=-1 \\ ij=k, ji=-k \\ jk=i, kj=-i \\ ki=j, ik=-j \end{cases} \]

用标量和向量表示四元数

\[ q=[s,v]^T,\quad s=q_0\in\mathbb{R},\quad v=[q_1,q_2,q_3]^T\in\mathbb{R^3} \]

\(s\)为四元数实部，\(v\)为四元数虚部，如果一个四元数的虚部为0，称之为实四元数。反之,若它的实部为0，则称之为虚四元数

乘以\(i\)意味着旋转180°，\(ij=k\)

坐标轴记忆，从xyz都为正的象限看向原点，xyz轴呈逆时针顺序

运算

\[ q_a=s_a +x_ai + y_aj + z_ak, \quad q_b=s_b+x_bi+y_bj+z_bk \]

加法减法

\[ q_a\pm q_b=[s_a\pm s_b, v_a\pm v_b]^T \]

乘法

每项分别相乘然后相加，总共16项，虚部乘法转换要按照运算关系

\[ \begin{align*} q_aq_b=&s_as_b-x_ax_b-y_ay_b-z_az_b\\ +&(s_ax_b+x_as_b+y_az_b-z_ay_b)i\\ +&(s_ay_b-x_az_b+y_as_b+z_ax_b)j\\ +&(s_az_b+x_ay_b-y_ax_b+z_as_b)k \end{align*} \]

\[ q_aq_b=[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a\times v_b]^T \]

乘法不具备交换律

模长

\[ \| q_a\|=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2} \]

四元数乘积的模长等于模长的乘积

\[ \|q_aq_b\|=\|q_a\|\|q_b\| \]

共轭

把虚部向量取反

\[ q_a^*=[s_a,-v_a]^T \]

\[ q^*q=qq^*=[s_a+v^Tv,0]^T \]

得到实四元数

\[ q^{-1}=q^*/\|q\|^2 \]

\[ q^{-1}q=qq^{-1}=1 \]

四元数为单位四元数，其逆和共轭是一个量

\[ q_I^{-1}=q_I^{*} \]

乘积的逆具有类似矩阵的性质

\[ (q_aq_b)^{-1}=q_b^{-1}q_a^{-1} \]

数乘

\[ kq=[ks,kv]^T \]

表示旋转

点用四元数描述

\[ p=[0,x,y,z]^T=[0,v]^T \]

旋转后的点为

\[ p'=qpq^{-1} \]

然后把\(p'\)虚部取出来

其他旋转转换到四元数

四元素乘法写成矩阵乘法

\[ q^+=\begin{bmatrix} s & -v^T\\ v & sI+v^\wedge \end{bmatrix}, \quad q^{\oplus}=\begin{bmatrix} s & -v^T\\ v & sI-v^\wedge \end{bmatrix} \]

\[ q_1^+q_2=\begin{bmatrix} s & -v^T\\ v & sI+v^\wedge \end{bmatrix} \begin{bmatrix} s_2\\ v_2 \end{bmatrix} = \begin{bmatrix} -v_1^Tv_2+s_1s_2\\ s_1v_2+s_2v_1+v_1^\wedge v_2 \end{bmatrix} = q_1q_2 \]

可以证明

\[ q_1q_2=q_1^+q_2=q_2^\oplus q_1 \]

\[ \begin{align*} p'=&qpq^{-1}=q^+p^+q^{-1}\\ =&q^+{q^{-1}}^\oplus p \end{align*} \]

带入矩阵计算

\[ q^+{(q^{-1})}^\oplus=\begin{bmatrix} s & -v^T \\ v & sI+v^\wedge \end{bmatrix} \begin{bmatrix} s & v^T \\ -v & sI+v^\wedge \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0^T & vv^T+s^2I+2sv^\wedge+(v^\wedge)^2 \end{bmatrix} \]

\[ R=vv^T+s^2I+2sv^\wedge+(v^\wedge)^2 \]

两边求迹

\[ \begin{align*} \mathrm{tr}(R)&=\mathrm{tr}\left (vv^T+s^2I+2sv^\wedge+(v^\wedge)^2\right)\\ &=v_1^2+v_2^2+v_3s^2+3s^2-2(v_1^2+v_2^2+v_3^2)\\ &=(1-s^2)+3s^2-2(1-s^2)\\ &=4s^2-1 \end{align*} \]

\[ \begin{align*} \theta&=\arccos\left(\frac{\mathrm{tr}(R-1)}{2}\right)\\ &=\arccos(2s^2-1) \end{align*} \]

\[ \begin{cases} \theta=2\arccos s\\ [n_1,n_2,n_3]^T=[q_1,q_2,q_3]^T/\sin\frac{\theta}{2} \end{cases} \]

3D变换

相似变换

\(R\)部分缩放

\[ T_s=\begin{bmatrix} sR &t\\ 0^T & 1 \end{bmatrix} \]

仿射

\(R\)矩阵不再正交，只要求可逆

\[ T_s=\begin{bmatrix} A &t\\ 0^T & 1 \end{bmatrix} \]

射影

\[ T_s=\begin{bmatrix} A &t\\ a^T & 1 \end{bmatrix} \]

\(A\)可逆，\(a^T\)缩放，\(t\)平移

Pangolin基于OpenGL的绘图库

李群与李代数

基础

群

\[ \mathrm{SO}(3)=\left \{\mathbf{R}\in \mathbb{R}^{3\times 3}|RR^T=I,\det(R)=1\right \} \]

\[ \mathrm{SE}(3)= \left \{T= \begin{bmatrix} R & t\\ 0^T & 1 \end{bmatrix} \in \mathbb{R}^{4\times 4} | R \in \mathrm{SO}(3), t\in \mathbb{R}^3 \right \} \]

对加法不封闭

\[ R_1+R_2\notin \mathrm{SO}(3),\quad T_1+T_2\notin\mathrm{SE}(3) \]

乘法是封闭的

\[ R_1R_2\in \mathrm{SO}(3),\quad T_1T_2\in\mathrm{SE}(3) \]

群（Group）是一种集合加上运算的代数结构，集合记为\(A\)，群记作\(G=(A,\cdot)\)，满足：

封闭性：\(\forall a_1,a_2\in A,\quad a_1\cdot a_2\in A\)
结合律：\(\forall a_1,a_2,a_3\in A,\quad (a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)\)
幺元：\(\exists a_0\in A,\quad \mathrm{s.t.}\quad \forall a\in A, \quad a_0\cdot a=a\cdot a_0=a\)
逆：\(\forall a\in A, \quad \exists a^{-1}\in A, \quad \mathrm{s.t.} \quad a\cdot a^{-1}=a_0\)

李群是指具有连续性质的群，整数\(\mathbb{Z}\)没有

李代数

对于旋转矩阵

\[ RR^T=I \]

\(R\)随时间变化，则

\[ R(t)R(t)^T=I \]

等式两边求导，得到：

\[ \dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0 \]

\[ \dot{R}(t)R(t)^T=-(R(t)\dot{R}(t)^T)^T \]

\(\dot{R(t)}R(t)^T\)是一个反对称矩阵，所以存在一个向量和反对称矩阵对应

\[ a^\wedge=A=\begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{bmatrix},\quad A^{\vee}=a \]

设这个三维向量为\(\phi(t)\in \mathbb{R}^3\)，则

\[ \dot{R}(t)R(t)^T=\phi(t)^\wedge \]

两边右乘\(R(t)\)得到

\[ \dot{R}(t)=\phi(t)^\wedge R(t)=\begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix} R(t) \]

\(R(t)\)在\(t=0\)附近的一阶泰勒展开

\[ \textit{\textbf{text}} \begin{align*} R(t)&\approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ &=I+\phi(t_0)^\wedge(t) \end{align*} \]

\(\phi\)反映了\(R\)的导数性质，故称它在\(\mathrm{SO}(3)\)原点附近的正切空间（Tangent Space）上，在\(t_0\)附近，有

\[ \dot{R}(t)=\phi(t_0)^\wedge R(t)=\phi_0^\wedge R(t) \]

解微分方程，类似于\(f'(x)=kf(x)\)，得到

\[ R(t)=e^{\phi_0^\wedge t} \]

总结：

给定某时刻的\(R\)就能求得一个\(\phi\)，\(\phi\)是对应到\(\mathrm{SO}(3)\)上的李代数\(\mathfrak{so}(3)\)
引出李群与李代数间的指数/对数映射

李代数定义

李代数由一个集合\(\mathbb{V}\)，一个数域\(\mathbb{F}\)和一个二元运算\([,]\)组成，如果它们满足以下几条性质，则称\((\mathbb{V},\mathbb{F},[,])\)为一个李代数，记作\(\mathfrak{g}\)。

封闭性 \(\forall X,Y\in\mathbb{V},[X,Y]\in\mathbb{V}\)
双线性 \(\forall X,Y,Z\in\mathbb{V},a,b\in\mathbb{F}\)，有

\[ [aX+bY,Z]=a[X,Z]+b[Y,Z],\quad [Z,aX+bY]=a[Z,X]+b[Z,Y] \]

自反性 \(\forall X\in\mathbb{V},[X,X]=0\)
雅可比等价 \(\forall X,Y,Z\in\mathbb{V},[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0\)

\[ \mathfrak{se}(3)=\left \{ \xi =\begin{bmatrix} \rho\\ \phi \end{bmatrix} \in \mathbb{R}^6, \rho\in\mathbb{R}^3, \phi\in\mathfrak{se}(3),\xi^\wedge=\ \begin{bmatrix} \phi^\wedge & \rho\\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4\times 4} \right \} \]

二元运算被称为李括号

李代数\(\mathfrak{so}(3)\)

\[ \mathit{\Phi}=\phi^\wedge=\begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix}\in\mathbb{R}^{3\times 3} \]

李括号的定义

\[ [\phi_1,\phi_2]=(\mathit{\Phi}_1\mathit{\Phi}_2-\mathit{\Phi}_2\mathit{\Phi}_1)^{\wedge} \]

六维向量，前三维平移（和矩阵不一样），记作\(\rho\)，后三维为旋转，记作\(\phi\)，对于\(\xi^\wedge\)，扩展了反对称的用法

\[ \xi^\wedge=\ \begin{bmatrix} \phi^\wedge & \rho\\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4\times 4} \]

\[ [\xi_1,\xi_2]=(\xi_1^\wedge\xi_2^\wedge-\xi_2^\wedge\xi_1^\wedge) \]

指数与对数映射

\(\mathfrak{so}(3)\)上的指数映射

任意矩阵的指数映射可以泰勒展开，在收敛的情况下仍然是一个矩阵

\[ \exp(A)=\sum^\infty_{n=0}\frac{1}{n!}A^n \]

\[ \exp(\phi^\wedge)=\sum^\infty_{n=0}\frac{1}{n!}(\phi^\wedge)^n \]

用向量定义\(\phi\)，有\(\phi=\theta a,\space\|a\|=1\)

\[ a^\wedge a^\wedge=\begin{bmatrix} -a_2^2-a_3^2 & a_1a_2 & a_1a_3\\ a_1a_2 & -a_1^2-a_3^2 & a_2a_3\\ a_1a_3 & a_2a_3 & -a_1^2-a_2^2 \end{bmatrix}=aa^T-I \]

\[ a^\wedge a^\wedge a^\wedge =a^\wedge(aa^T-I)=-a^\wedge \]

由此可以得到\(a^\wedge\)的n次的结果

\[ \begin{align*} \exp(\phi^\wedge)&=\sum^\infty_{n=0}\frac{1}{n!}(\theta a^\wedge)^n\\ &=I+\theta a^\wedge-a^\wedge a^\wedge + \theta a^\wedge + \frac{1}{2!}\theta^2 a^\wedge a^\wedge +\frac{1}{3!} (a^\wedge)^3 +\frac{1}{4!} (a^\wedge)^4 + \ldots\\ &=aa^T- a^\wedge a^\wedge +\theta a^\wedge + \frac{1}{2!}\theta^2 a^\wedge a^\wedge -\frac{1}{3!} a^\wedge -\frac{1}{4!} (a^\wedge)^2\\ &=aa^T+\sideset{}{}{\underbrace{\left( \theta - \frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+\ldots \right )}}_{\sin \theta}a^\wedge-\sideset{}{}{\underbrace{\left( 1 - \frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+\ldots \right )}}_{\cos \theta}a^\wedge a^\wedge\\ &=a^\wedge a^\wedge + I+\sin\theta a^\wedge - \cos\theta a^\wedge a^\wedge\\ &=(1-\cos\theta)a^\wedge a^\wedge+I+\sin\theta a^\wedge\\ &=\cos\theta+(1-\cos\theta)aa^T+\sin\theta a^\wedge \end{align*} \]

最后得到：

\[ \exp(\theta a^\wedge)=\cos\theta+(1-\cos\theta)aa^T+\sin\theta a^\wedge \]

和罗德公式一样

\(\mbox{SE}(3)\)上的指数映射

\[ \begin{align*} \exp{\xi^\wedge}&=\begin{bmatrix} \sum_{n=0}^{\infty}\frac{1}{n!}(\phi^\wedge)^n & \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^\wedge)^n\rho\\ 0^T & 1 \end{bmatrix} \\ &\triangleq\begin{bmatrix} R & J\rho\\ 0^T & 1 \end{bmatrix} = T \end{align*} \]

同样的展开方式求得

\[ J=\frac{\sin\theta}{\theta}I+\left(1-\frac{\sin\theta}{\theta}\right)aa^T+\frac{1-\cos\theta}{\theta}a^\wedge \]

最后总结李群和李代数的关系

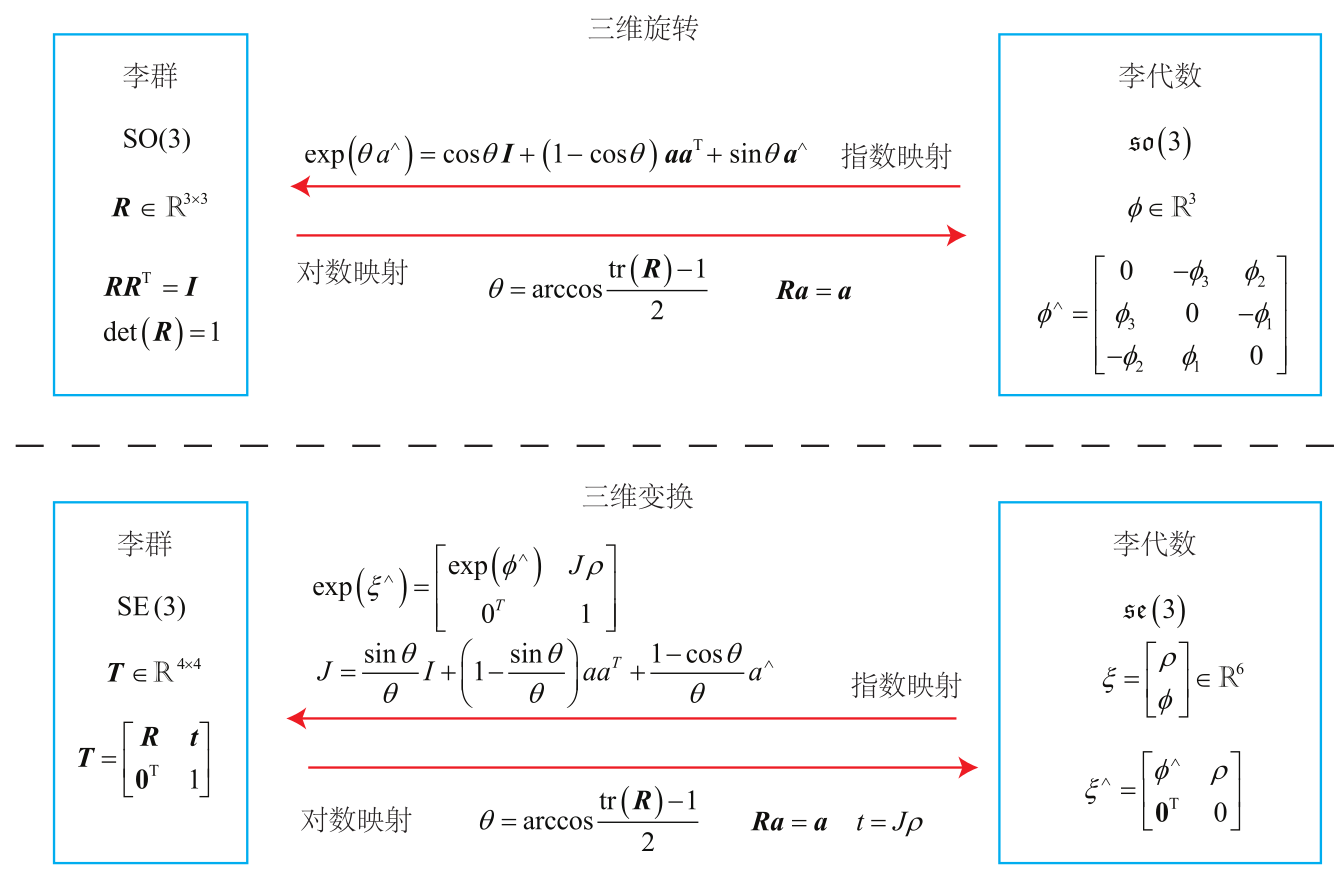
李代数求导和扰动模型

Sophus

相机与图像

相机模型

透镜产生畸变，根据模型计算内参

针孔相机模型

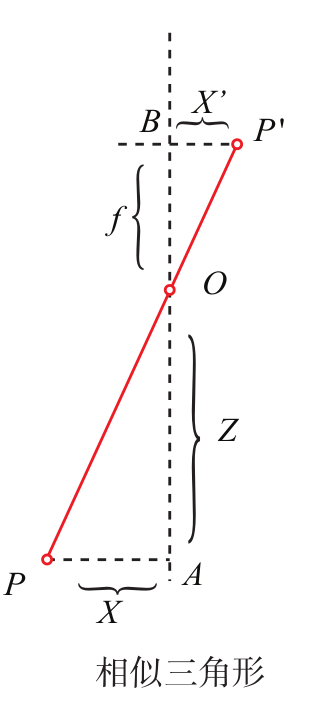
\(X\)为物体大小，\(X'\)为图像大小

\[ \frac{Z}{f}=-\frac{X}{X'}=-\frac{Y}{Y'} \]

所以得到

\[ \begin{cases} X'=f\frac{X}{Z}\\ Y'=f\frac{Y}{Z} \end{cases} \]

像素坐标：

\[ [u,v]^T \]

原点定义为图像的左上角，和成像平面多了缩放和原点的平移

所以得到

\[ \begin{cases} u=\alpha X'+c_x\\ v=\beta Y' + c_y \end{cases} \]

\[ \begin{cases} u=f_x \frac{X}{Z}+c_x\\ v=f_y \frac{Y}{Z} + c_y \end{cases} \]

改成齐次坐标变换

\[ \begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\triangleq\frac{1}{Z}KP \]

\[ Z\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\begin{pmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\triangleq KP \]

\(K\)为内参矩阵，一般出厂后是固定的，标定方法有单目棋盘格张正友标定法

相机的外参\(R,t\)为相机的旋转平移量，\(P=RP_w+t\)

投影过程可以看成把世界坐标点转换到相机坐标系，再去掉相机z轴方向的数值

畸变

透镜形状引起的畸变称为径向畸变，分为桶形畸变和枕形畸变

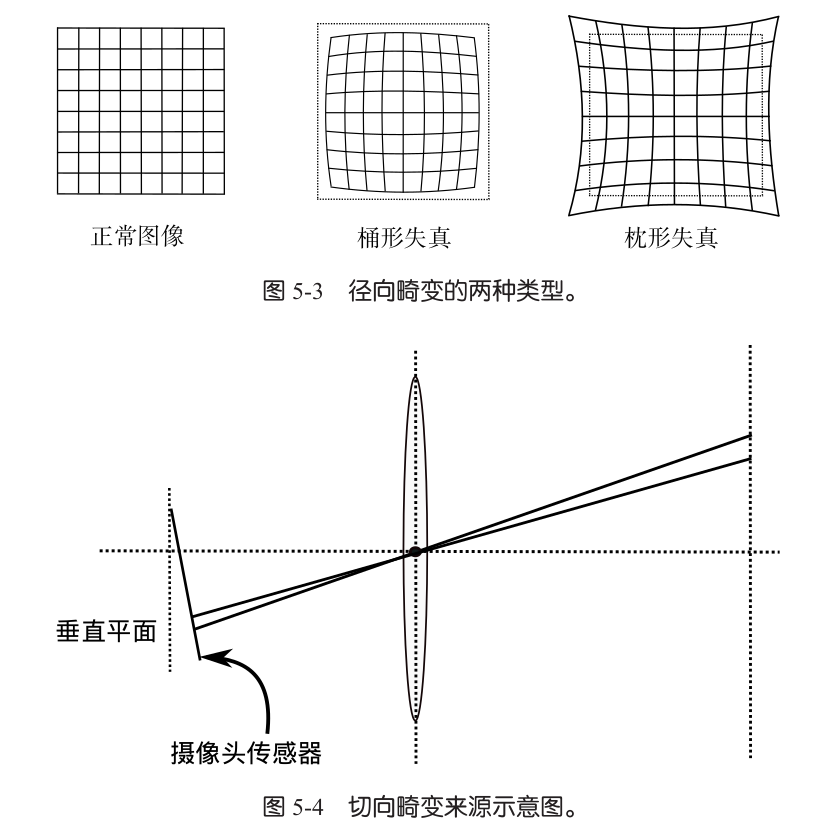
畸变.png

切向畸变来源为透镜和成像平面不平行

径向畸变多项式关系：

\[ \begin{align} x_\text{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\ y_\text{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{align} \]

对于切向畸变，用另外的参数纠正：

\[ \begin{align} x_\text{distorted}=x + 2p_1xy+p_2(r^2+2x^2)\\ y_\text{distorted}=x + 2p_2xy+p_1(r^2+2y^2) \end{align} \]

三维空间归一化坐标为\([x,y]^T\)
径向畸变和切向畸变

\[ \begin{cases} x_\text{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)\\ y_\text{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{cases} \]

通过内参矩阵变换到像素平面

\[ \begin{cases} u=f_xx_\text{distorted}+c_x\\ v=f_yy_\text{distorted}+c_y \end{cases} \]

双目相机模型

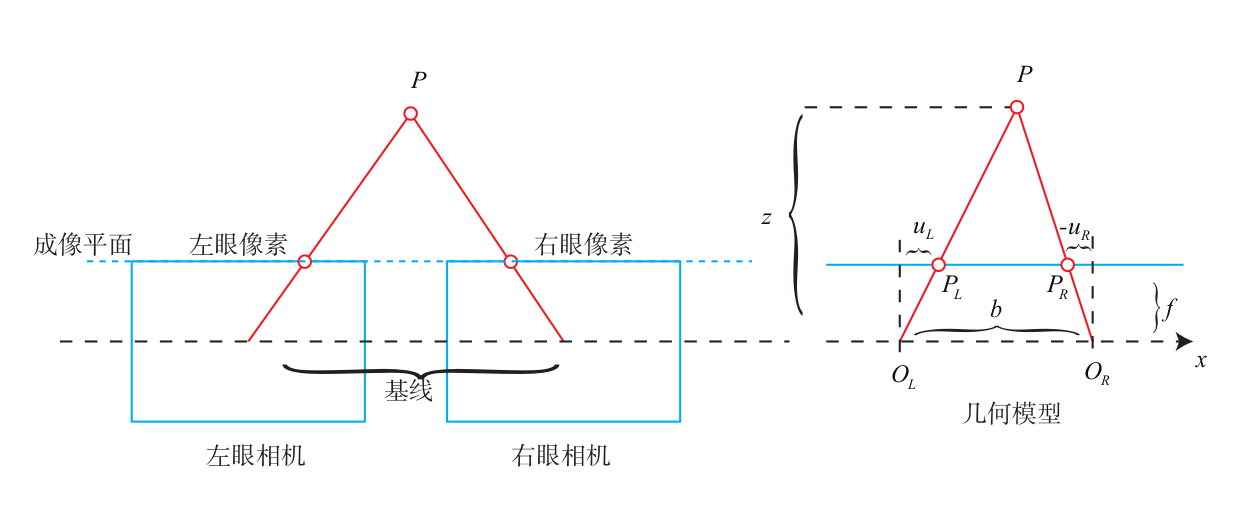\[ \frac{z-f}{z}=\frac{b-u_L+u_R}{b} \]

\[ z=\frac{fb}{d},\quad d\triangleq u_L-u_R \]

\(d\)为视差，成像物体在中间，所以两边图像要看上去一样其中一张需要水平翻转，同一物体在两张图片中的横坐标差值（左右相机横放），视差越大距离越近，基线大的测得的最大距离越远，小的能够测量近处距离

RGB-D相机模型

红外结构光
飞行时间法(Time-of-flight,ToF)

实例

图像去畸变

opencv自带cv::Undistort()

每个点用公式计算一遍，颜色换算过去，但是要保证每个像素都有颜色，就必须使用去畸变后的每个图像位置去映射之前的图像中的像素

image_undistort.at<uchar>(v, u) = image.at<uchar>((int) v_distorted, (int) u_distorted);

双目视觉

cv::StereoSGBM把左右图转为深度图，然后根据深度信息和两张原图拉伸成立体点云

RGB-D

非线性优化

状态估计问题

批量状态估计与最大后验估计

运动方程和观测方程

\[ \begin{cases} x_k=f(x_{k-1},u_k)+w_k\\ z_{k,j}=h(y_i,x_k)+v_{k,j} \end{cases} \]

\(x_k\)为相机位姿，用\(\text{SE}(3)\)描述

观测方程可以表示成：

\[ sz_{k,j}=K(R_ky_j+t_k) \]

\(K\)为相机内参，\(s\)为像素点距离（物体到镜头），被观测的物体发生\(R_k\)旋转和\(t_k\)平移

假设噪声\(w_k,v_{k,j}\)满足零均值高斯分布

\[ w_k\sim\mathcal{N}(0,R_k),v_k\sim\mathcal{N}(0,Q_{k,j}) \]

\(\mathcal{N}\)表示高斯分布，\(0\)表示零均值，\(R_k,Q_{k,j}\)表示协方差矩阵，在有噪声情况根据\(z\)和\(u\)推断位姿\(x\)和地图\(y\)，构成状态估计问题

两种方式：

用当前时刻估计来估计后来的数据，增量/渐进，滤波器，扩展卡尔曼滤波（EKF）
批量一次性处理数据

折中方法：滑动窗口估计

考虑从\(1\)到\(N\)的所有时刻，假设有\(M\)个路标点。所有时刻机器人位姿和路标为

\[ x=\{x_1,\ldots,x_N\},\quad y=\{y_1,\ldots,y_M\} \]

用不带下标的\(u\)表示所有时刻输入，\(z\)表示所有时刻的观测数据，对机器人状态估计。已知输入数据\(u\)和观测数据\(z\)的条件下，求状态\(x,y\)的条件概率分布：

\[ P(x,y|z,u) \]

当输入数据不变，变为重建三维空间结构的问题，\(P(x,y|z)\)，Structure from Motion（SfM）

根据贝叶斯法则：

\[ P(x,y|z,u)=\frac{P(z,u|x,y)P(x,y)}{P(z,u)}\propto \sideset{}{}{\underbrace{P(z,u|x,y)}}_{似然} \space \sideset{}{}{\underbrace{P(x,y)}}_{先验} \]

未完

视觉里程计

特征点法

提取图像里面一些特别的地方

角点：Harris、FAST、GFTT
局部特征：SIFT、SURF、ORB（人工设计的特征点）

SIFT（尺度不变特征变换，Scale-Invariant Feature Transform）

ORB（Oriented FAST and Rotated BRIEF）

FAST关键点

选取像素\(p\)，假设亮度为\(I_p\)
设置阈值\(T\)（比如，\(I_p\)的20%）
以像素\(p\)为中心，选取半径为3的圆上16个像素点
假如选取的圆上有连续的\(N\)个点的亮度大于\(I_p+T\)或小于\(I_p-T\)，那么像素\(p\)可以被认为是特征点（\(N\) 通常取 12，即为 FAST-12。其他常用的\(N\)取值为 9 和 11，它们分别被称为 FAST-9 和 FAST-11）
循环以上四步,对每一个像素执行相同的操作

FAST-12算法更高效的排除不是角点的像素，在邻域圆上第1,5,9,13的像素，只有4个中有3个同时大于\(I_p+T\)或小于\(I_p-T\)，当前像素才有可能是角点

BRIEF描述子

特征匹配

暴力匹配
快速近似最临近（FLANN）

ORB特征

2D-2D：对极几何

对极约束

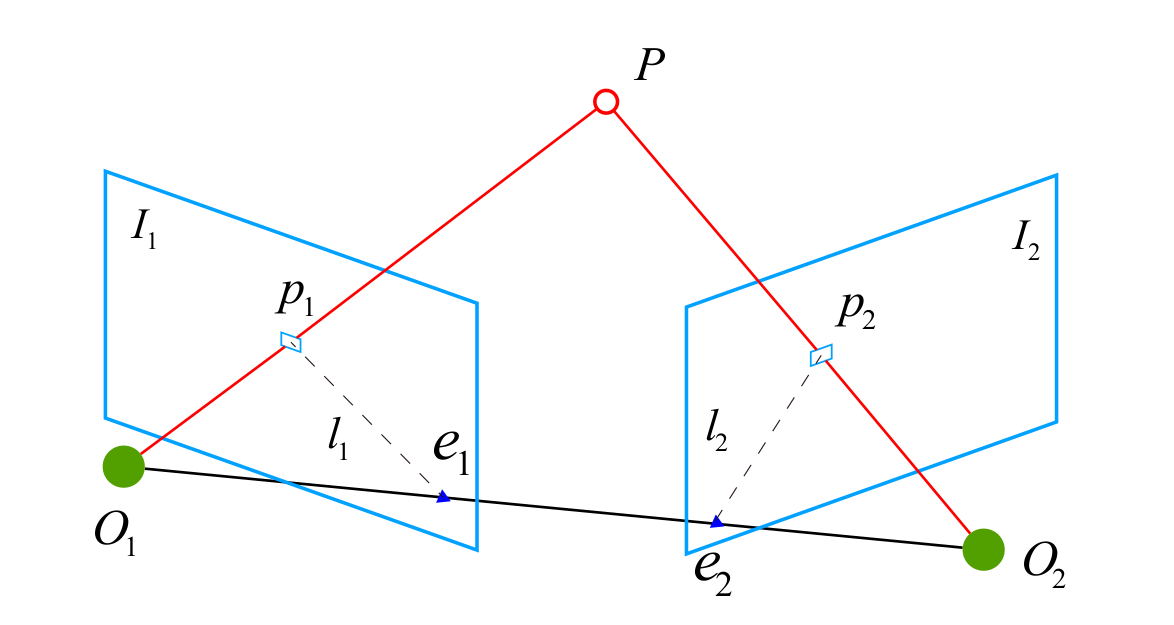
如果特征点匹配正确，\(O_1,p_1,P,O_2,p_2\)为同一平面上，称为极平面（Epipolar plane），和像平面的交点\(e_1,e_2\)称为极点（Epipoles），\(O_1O_2\)称为基线（Baseline），\(l_1,l_2\)为极线（Epipolar line）

\[ P=[X,Y,Z]^T \]

两个像素点的位置为

\[ s_1p_1=KP,\quad s_2p_2=K(RP+t) \]

\(s_1p_1\)和\(p_1\)构成投影关系，齐次坐标意义下是相等的，成为尺度意义下的相等

\[ sp\simeq p \]

投影关系写作

\[ p_1\simeq KP,\quad p_2\simeq K(RP+t) \]

取

\[ x_1=K^{-1}p_1,\quad x_2=K^{-1}p_2 \]

带入上个公式

\[ x_2\simeq Rx_1+t \]

两边左乘\(t^\wedge\)，相当于两边和\(t\)外积

\[ t^\wedge x_2 = t^\wedge Rx_1 \]

两边左乘\(x_2^T\)

\[ x_2^Tt^\wedge x_2\simeq x_2^Tt^\wedge Rx_1 \]

左边\(t^\wedge x_2\)是和\(t\)和\(x_2\)垂直的向量，再做内积得到0,

\[ x_2^Tt^\wedge Rx_1=0 \]

代入\(p_1,p_2\)

\[ p_2^TK^{-T}t^\wedge RK^{-1}p_1=0 \]

称为对极约束，几何意义为\(O_1,P,O_2\)三者共面，把中间部分记为两个矩阵：基础矩阵（Fundamental Matrix）\(F\)和本质矩阵（Essential Matrix）\(E\)，简化为

\[ E=t^\wedge R,\quad F=K^{-T}EK^{-1}, \quad x_2^TEx_1=p_2^TFp_1=0 \]

位姿估计两步：

根据配对的像素点求出\(E\)或者\(F\)
根据\(E\)或者\(F\)求出\(R,t\)

本质矩阵

八点法求解\(E\)，\(x_1=[u_1,v_1,1]^T,x_2=[u_2,v_2,1]^T\)

\[ (u_2,v_2,1)\begin{pmatrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{pmatrix}\begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} = 0 \]

\[ u_2u_1e_1+u_2v_1e_2+u_2e_3+u_1v_2e_4+v_1v_2e_5+v_2e_6+u_1e_7+v_1e_8+e_9=0 \]

\[ \left [u_2u_1,u_2v_1,u_2,u_1v_2,v_1v_2,v_2,u_1,v_1,1\right ]\cdot e=0 \]

放到方程组里面

\[ \begin{pmatrix} u_2^2u_1^2&u_2^2v_1^2&u_2^2&u_1^2v_2^2&v_1^2v_2^2&v_2^2&u_1^2&v_1^2&1\\ u_2^2u_1^2&u_2^2v_1^2&u_2^2&u_1^2v_2^2&v_1^2v_2^2&v_2^2&u_1^2&v_1^2&1\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ u_2^8u_1^8&u_2^8v_1^8&u_2^8&u_1^8v_2^8&v_1^8v_2^8&v_2^8&u_1^8&v_1^8&1 \end{pmatrix} = \begin{pmatrix} e_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6\\ e_7\\ e_8 \end{pmatrix} = 0 \]

如果系数矩阵是满秩的（即秩为 8）,那么它的零空间维数为 1

一个矩阵A的列秩是A的线性独立的纵列的极大数，通常表示为r(A)，rk(A)或rank A，通常把满秩矩阵叫做可逆矩阵，det(A)≠0，不满秩的矩阵叫做奇异矩阵，det(A)=0

经过奇异值分解（SVD）

\[ E=U\Sigma V^T \]

\(U,V\)为正交矩阵，\(\Sigma\)为奇异值矩阵

奇异值分解（SVD）https://zhuanlan.zhihu.com/p/29846048

根据\(E\)的内在性质，\(\Sigma=\text{diag}(\sigma,\sigma,0)\)，在 SVD分解中，对于任意一个 E，存在两个可能的 \(t,R\) 与它对应：

\[ \begin{align} t_1^\wedge=UR_Z(\frac{\pi}{2})\Sigma U^T, \quad R_1=UR_Z^T(\frac{\pi}{2})V^T\\ t_2^\wedge=UR_Z(-\frac{\pi}{2})\Sigma U^T, \quad R_2=UR_Z^T(-\frac{\pi}{2})V^T \end{align} \]

diag代表根据对角元素创建矩阵

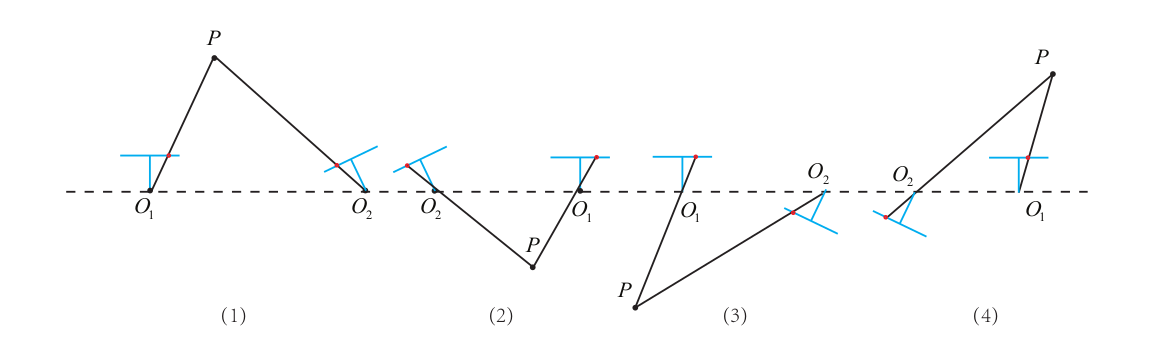
\(R_Z(\frac{\pi}{2})\)表示沿 \(Z\) 轴旋转 \(90\degree\) 得到的旋转矩阵。由于\(-E\)和\(E\)等价，所以对任意一\(t\)取负号得到同样结果，因此，从\(E\)分解到\(t,R\)时存在4个可能的解

单应矩阵

场景中的特征点都落在同一平面（比如墙壁和地面等），平面方程满足

\[ n^TP+d=0 \]

\(n\)是平面法向量，\(P\)是世界坐标原点到P的向量，点积为负，加上原点到平面距离为0，整理后得到

\[ -\frac{n^TP}{d}=1 \]

代入运动方程：

\[ s_1p_1=KP,\quad s_2p_2=K(RP+t) \]

\[ \begin{align} p_2 &\simeq K(RP+t)\\ &\simeq K\left(RP+t\cdot\left(-\frac{n^TP}{d}\right)\right)\\ &\simeq K\left(R-\frac{tn^T}{d}\right)P\\ &\simeq K\left(R-\frac{tn^T}{d}\right)K^{-1}p_1 \end{align} \]

得到\(p_1\)和\(p_2\)之间的变换，记作\(H\)

\[ p_2\simeq Hp_1 \]

类似用矩阵元素方式表示

\[ \begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} = k\begin{pmatrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \end{pmatrix}\begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} \]

\[ \begin{align} u_2=k(h_1u_1+h_2v_1+h_3)\\ v_2=k(h_4u_1+h_5v_1+h_6)\\ 1=k(h_7u_1+h_8v_1+h_9)\\ \end{align} \]

最后

\[ \begin{align} u_2=\frac{h_1u_1+h_2v_1+h_3}{h_7u_1+h_8v_1+h_9}\\ v_2=\frac{h_4u_1+h_5v_1+h_6}{h_7u_1+h_8v_1+h_9} \end{align} \]

通常乘以非零因子使得\(h_9=1\)，整理得：

\[ \begin{align} h_1u_1+h_2v_1+h_3-h_7u_1u_2-h_8v_1u_2=u_2\\ h_4u_1+h_5v_1+h_6-h_7u_1v_2-h_8v_1v_2=v_2 \end{align} \]

通过4对匹配特征点解线性方程组

\[ \begin{pmatrix} u_1^1 & v_1^1 & 1 & 0 & 0 & 0 & -u_1^1u_2^1 & -v_1^1u_2^1\\ 0 & 0 & 0 & u_1^1 & v_1^1 & 1 & -u_1^1v_2^1 & -v_1^1v_2^1\\ u_1^2 & v_1^2 & 1 & 0 & 0 & 0 & -u_1^2u_2^2 & -v_1^2u_2^2\\ 0 & 0 & 0 & u_1^2 & v_1^2 & 1 & -u_1^2v_2^2 & -v_1^2v_2^2\\ u_1^3 & v_1^3 & 1 & 0 & 0 & 0 & -u_1^3u_2^3 & -v_1^3u_2^3\\ 0 & 0 & 0 & u_1^3 & v_1^3 & 1 & -u_1^3v_2^3 & -v_1^3v_2^3\\ u_1^4 & v_1^4 & 1 & 0 & 0 & 0 & -u_1^4u_2^4 & -v_1^4u_2^4\\ 0 & 0 & 0 & u_1^4 & v_1^4 & 1 & -u_1^4v_2^4 & -v_1^4v_2^4 \end{pmatrix}\begin{pmatrix} h_1\\ h_2\\ h_3\\ h_4\\ h_5\\ h_6\\ h_7\\ h_8\\ \end{pmatrix}= \begin{pmatrix} u_2^1\\ v_2^1\\ u_2^2\\ v_2^2\\ u_2^3\\ v_2^3\\ u_2^4\\ v_2^4 \end{pmatrix} \]

数学问题表述#

三维空间刚体运动#

矩阵变换#

旋转向量和欧拉角#

欧拉角#

四元数#

3D变换#

李群与李代数#

基础#

群#

李代数#

指数与对数映射#

李代数求导和扰动模型#

Sophus#

相机与图像#

相机模型#

针孔相机模型#

畸变#

双目相机模型#

RGB-D相机模型#

实例#

图像去畸变#

双目视觉#

RGB-D#

非线性优化#

状态估计问题#

批量状态估计与最大后验估计#

视觉里程计#

特征点法#

2D-2D：对极几何#

对极约束#

本质矩阵#

单应矩阵#