说明
绝大部分内容来自 https://www.kalmanfilter.net ,可以直接去看英文版本
背景知识
均值和期望值
当系统状态可观测时,均值(Mean)代表平均水平
当系统测量值存在误差时,用期望值(Expected Value)估计真实值
方差标准差
方差
$$ \sigma^2=\frac{1}{N}\sum^N_{n=1}(x_n-\mu)^2 $$标准差
$$ \sigma $$正态分布
许多自然现象都遵循正态分布(Normal Distribution),又名高斯分布
$$ f(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2} }e^{\frac{-(x-\mu)^2}{2\sigma^2} } $$高斯函数被称为正态分布的概率密度函数(PDF)
随机变量
测量值都是连续随机变量
估计,准确度和精度
估计(Estimate)用来估算系统的不可见状态,比如用雷达估计飞行物的位置
准确度(Accuracy)测量值和真实值的接近程度
精密度(Precision)测量结果的再现性
精密度高,值的聚集程度高;准确度高,值离真实值更近
有偏(biased)系统存在固定系统误差
$\alpha-\beta-\gamma$滤波
例子1-金条重量
重量估计
估计静态系统,金条的重量,测量没有系统误差,存在随机噪声
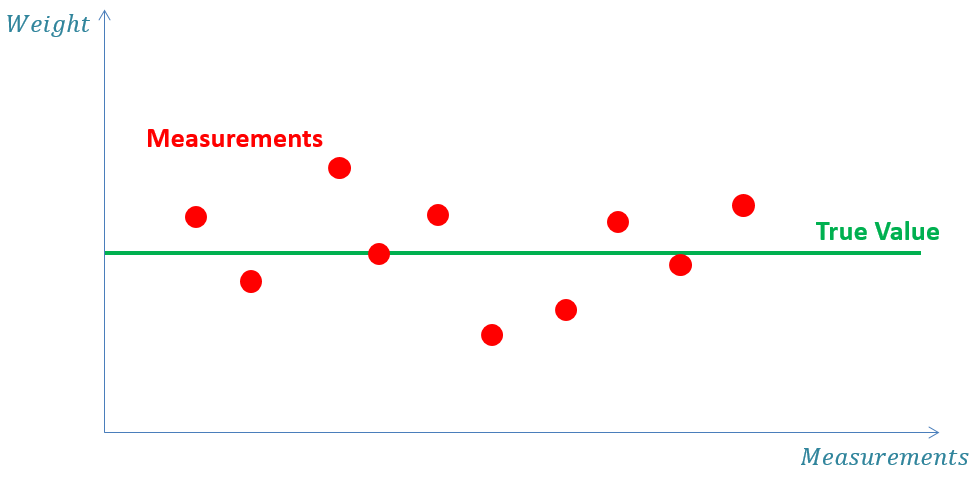
第N次的估计值为前面的测量值
$$ \hat{x}_{N,N}=\frac{1}{N}(z_1+z_2+...+z_{N-1}+z_N)=\frac{1}{N}\sum^N_{n=1}(z_n) $$符号
$x$ 重量的真实值
$z_n$ 第$n$次的测量值
$\hat{x}_{n,n}$ $x$第$n$次的估计值(在得到$z_n$之后的估计)
$\hat{x}_{n,n-1}$ $x$第$n-1$次的估计值(在拿到测量值$z_{n-1}$后)
$\hat{x}_{n+1,n}$ $x$未来$n+1$状态的估计值(在第$n$次时,在测量$z_n$后。换句话说是一个预测状态
带$\hat{x}$的值表示估计值
该例子中的动态模型是不变的,所以$x_{n+1,n}=x_{n,n}$
为了估计$\hat{x}_{N,N}$,我们需要记住历史测量值
| 说明 | |
|---|---|
| $\hat{x}_{N,N}=\frac{1}{N}\sum_{n=1}^N(z_n)=$ | 求N个测量值的均值 |
| $=\frac{1}{N}\left ( \sum_{n=1}^{N-1}(z_n)+z_N \right)=$ | 求前面N-1个测量值和最后一个测量值的和除以N |
| $=\frac{1}{N}\sum_{n=1}^{N-1}\left(z_n\right)+\frac{1}{N}z_N=$ | 展开 |
| $= \frac{1}{N}\frac{N-1}{N-1} \sum _{n=1}^{N-1} \left( z_{n} \right) + \frac{1}{N} z_{N} =$ | 乘以除以N-1 |
| $\frac{N-1}{N}{\color{ #FF8C00 }{\frac{1}{N-1} \sum _{n=1}^{N-1} \left( z_{n} \right)} } + \frac{1}{N} z_{N} =$ | 重新排序,颜色部分是之前的估计值 |
| $= \frac{N-1}{N}{\color{ #FF8C00 }{\hat{x}_{N,N-1} } } + \frac{1}{N} z_{N} =$ | 重写求和 |
| $= \hat{x}_{N,N-1}- \frac{1}{N}\hat{x}_{N,N-1}+ \frac{1}{N} z_{N} =$ | 展开分数 |
| $= \hat{x}_{N,N-1}+ \frac{1}{N} \left( z_{N}- \hat{x}_{N,N-1} \right)$ | 重新排序 |
$\hat{x}_{N,N-1}$ 是在N时刻的基于在N-1时刻的测量数据的x的预测,也就是之前的估计
最后的方程为卡尔曼滤波方程五个之一,第一个,为状态更新方程
$$ \hat{x}_{N,N}=\hat{x}_{N,N-1}+\frac{1}{N} \left( z_{N}- \hat{x}_{N,N-1} \right) $$$$ 当前状态的估计=当前状态的预测值+因子\times(测量值-当前状态的预测值) $$该因子被称作卡尔曼增益(Kalman Gain),表示为$K_n$,$n$表示该因子可以随着每次迭代发生改变,在深入讲解之前使用$\alpha_n$代替$K_n$,状态更新方程变为
$$ \hat{x}_{n,n}=\hat{x}_{n,n-1}+\alpha_n(z_n-\hat{x}_{n,n-1}) $$$(z_n-\hat{x}_{n,n-1})$被称为测量残差,也叫作更新(innovation),包含了新的信息
卡尔曼滤波需要预设一个初始猜测值,不用很精准
估计算法
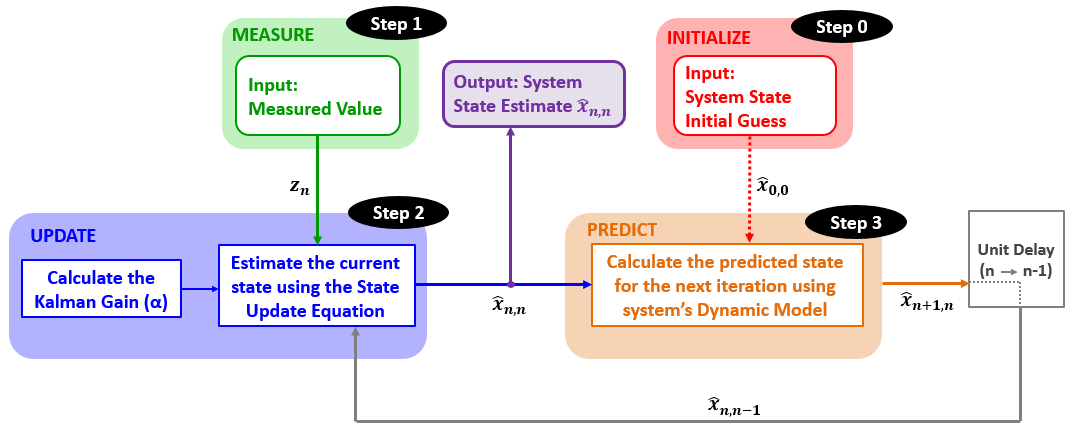
代码
import matplotlib.pyplot as plt
true = []
measure = [1030, 989, 1017, 1009, 1013, 979, 1008, 1042, 1012, 1011]
estimate = []
predict = 1000
def calculate():
global predict
for i in range(0, len(measure)):
alpha = 1 / (i + 1)
predict = predict + alpha * (measure[i] - predict)
estimate.append(predict)
true.append(1010)
return predict
if __name__ == '__main__':
calculate()
plt.plot(range(1, 11), true, label="True Value")
plt.plot(range(1, 11), measure, label="Measurements")
plt.plot(range(1, 11), estimate, label="Estimates")
plt.legend(loc='upper left')
plt.show()
得到结果
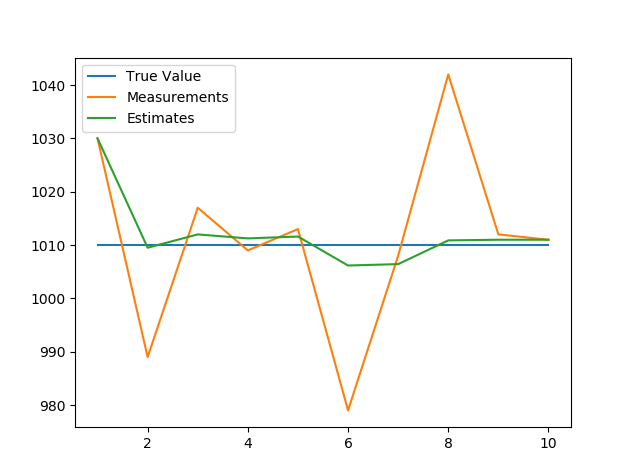
例子2-在一维空间中追踪匀速飞行器
使用$\alpha-\beta$滤波器在一维空间中追踪匀速飞行的飞行器
$x_n$代表飞行器在$n$时的航程
$$ \dot{x}=v=\frac{\text{d}x}{\text{d}t} $$雷达的发射周期为$\Delta t$,假设飞行器速度恒定,可以用两个运动方程描述
$$ \begin{array}{c} x_{n+1}=x_n+\Delta t\dot{x}_n\\ \dot{x}_{n+1}=\dot{x}_n \end{array} $$上述方程组称为状态外推方程(State Extrapolation Equation),也称过渡方程(Transition Equation)或者预测方程(Prediction Equation),卡尔曼五个滤波方程之一,第二个。在第一个例子中$x_{n+1}=x_n$为预测方程
$\alpha-\beta$滤波器
有些地方也叫$g-h$滤波器
速度的状态更新方程
$$ \hat{\dot x}_{n,n}=\hat{\dot x}_{n,n-1}+\beta\left( \frac{z_n-\hat{x}_{n,n-1} }{\Delta t} \right) $$位置的状态更新方程
$$ \hat{x}_{n,n}=\hat{x}_{n,n-1}+\alpha(z_n-\hat{x}_{n,n-1}) $$得到的状态方程组称为$\alpha-\beta$轨迹更新方程(track update equation)或者轨迹滤波方程(track filtering equation)
估计算法
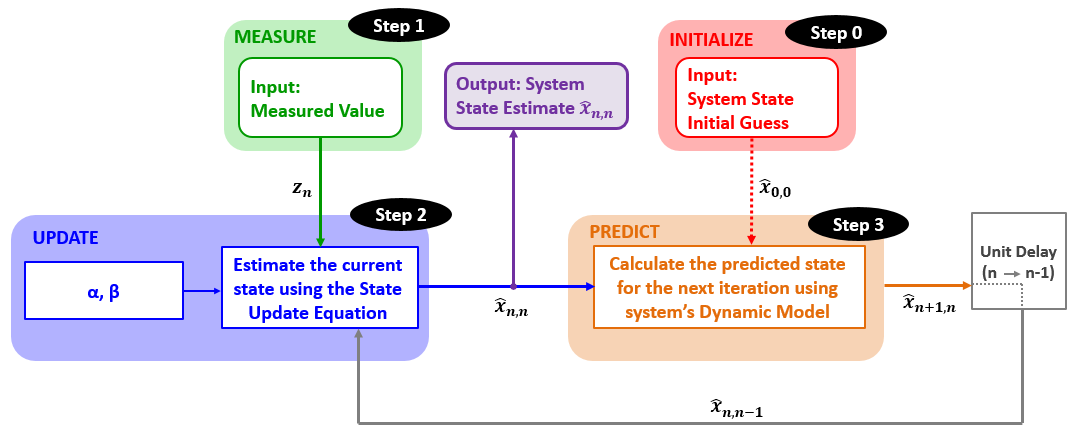
代码
import matplotlib.pyplot as plt
true = []
measure = [30110, 30265, 30740, 30750, 31135, 31015, 31180, 31610, 31960, 31865]
predict_speed_n = 40
predict_pos_n = 30200
alpha = 0.2
beta = 0.1
delta_t = 5.0
estimate_speed = []
estimate_pos = []
predict_speed = []
predict_pos = []
x = []
def calculate():
global predict_pos_n, predict_speed_n
for i in range(0, len(measure)):
# 估计
pos = predict_pos_n + alpha * (measure[i] - predict_pos_n)
speed = predict_speed_n + beta * (measure[i] - predict_pos_n) / delta_t
# 记录
predict_speed.append(predict_speed_n)
predict_pos.append(predict_pos_n)
estimate_speed.append(speed)
estimate_pos.append(pos)
true.append(30000 + 40 * (i + 1) * delta_t)
x.append((i + 1) * delta_t)
# 预测
predict_pos_n = pos + speed * delta_t
predict_speed_n = speed
if __name__ == '__main__':
calculate()
plt.plot(x, true, label="True Value")
plt.plot(x, measure, label="Measurements", marker='.')
plt.plot(x, estimate_pos, label="Estimates", marker='.')
plt.plot(x, predict_pos, label="Predict", marker='^')
plt.legend(loc='upper left')
plt.show()
得到结果
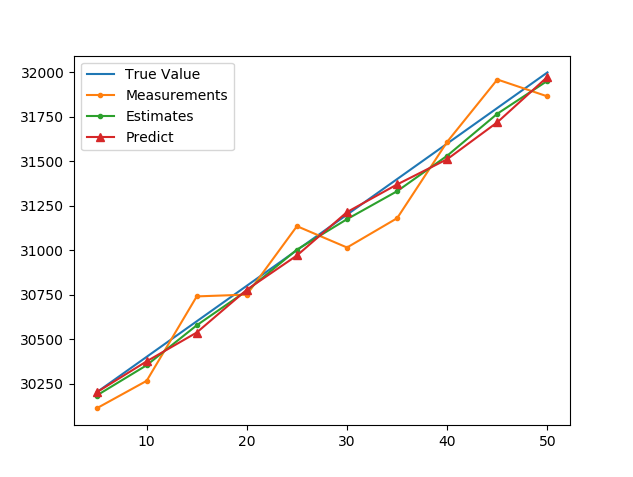
对于测量精度较高的系统,可以采用较大的$\alpha,\beta$,测量权值更高,会更快的对系统测量做出反应。而测量精度较低的系统,采用较低的$\alpha,\beta$,滤波器降低测量中的不确定性,对目标的变化反应慢很多
例子3 – 在一维空间中追踪加速飞行器
对于加速度一定的目标
速度在15s后进行匀加速运动,输入测量值
measure = [30200, 30400, 30600, 30900, 31400, 32100, 33000, 34100, 35400, 36900, 38600, 40500, 42600, 44900, 47400, 50100]得到的图像与测量值存在滞后,有一个固定误差叫滞后误差(lag error)
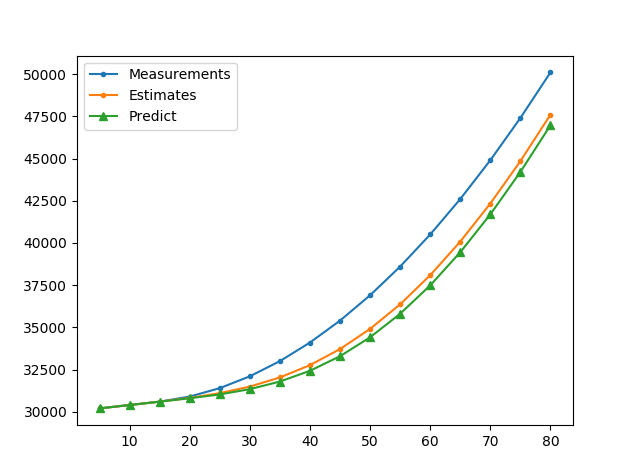
滞后误差的其他名称有:
- 动态误差 Dynamic error
- 系统误差 Systematic error
- 偏移误差 Bias error
- 截断误差 Truncation error
例子4 – 用$\alpha-\beta-\gamma$滤波器追踪加速飞行器
也叫($g-h-k$滤波器),考虑加速度,状态方程变为
$$ \begin{array}{c} \hat{x}_{n,n}=~ \hat{x}_{n,n-1}+ \alpha \left( z_{n}- \hat{x}_{n,n-1} \right)\\ \hat{\dot{x} }_{n,n}= \hat{\dot{x} }_{n,n-1}+ \beta \left( \frac{z_{n}-\hat{x}_{n,n-1} }{ \Delta t} \right)\\ \hat{\ddot{x} }_{n,n}= \hat{\ddot{x} }_{n,n-1}+ \gamma \left( \frac{z_{n}-\hat{x}_{n,n-1} }{0.5 \Delta t^{2} } \right) \end{array} $$代码
import matplotlib.pyplot as plt
measure = [30160, 30365, 30890, 31050, 31785, 32215, 33130, 34510, 36010, 37265]
# measure = [30110, 30265, 30740, 30750, 31135, 31015, 31180, 31610, 31960, 31865]
true = [30250, 30500, 30750, 31100, 31650, 32400, 33350, 34500, 35850, 37400]
predict_speed_n = 50
predict_pos_n = 30250
predict_acc_n = 0
alpha = 0.5
beta = 0.4
gamma = 0.1
delta_t = 5.0
estimate_speed = []
estimate_pos = []
estimate_acc = []
predict_speed = []
predict_pos = []
predict_acc = []
x = []
def calculate():
global predict_pos_n, predict_speed_n, predict_acc_n
for i in range(0, len(measure)):
# 估计
pos = predict_pos_n + alpha * (measure[i] - predict_pos_n)
speed = predict_speed_n + beta * (measure[i] - predict_pos_n) / delta_t
acc = predict_acc_n + gamma * (measure[i] - predict_pos_n) / (0.5 * delta_t * delta_t)
# 记录
predict_speed.append(predict_speed_n)
predict_pos.append(predict_pos_n)
predict_acc.append(predict_acc_n)
estimate_speed.append(speed)
estimate_pos.append(pos)
estimate_acc.append(acc)
x.append((i + 1) * delta_t)
# 预测
predict_pos_n = pos + speed * delta_t + acc * 0.5 * delta_t * delta_t
predict_speed_n = speed + acc * delta_t
predict_acc_n = acc
if __name__ == '__main__':
calculate()
plt.plot(x, true, label="True Value")
plt.plot(x, measure, label="Measurements", marker='.')
plt.plot(x, estimate_pos, label="Estimates", marker='.')
plt.plot(x, predict_pos, label="Predict", marker='^')
plt.legend(loc='upper left')
plt.show()得到结果
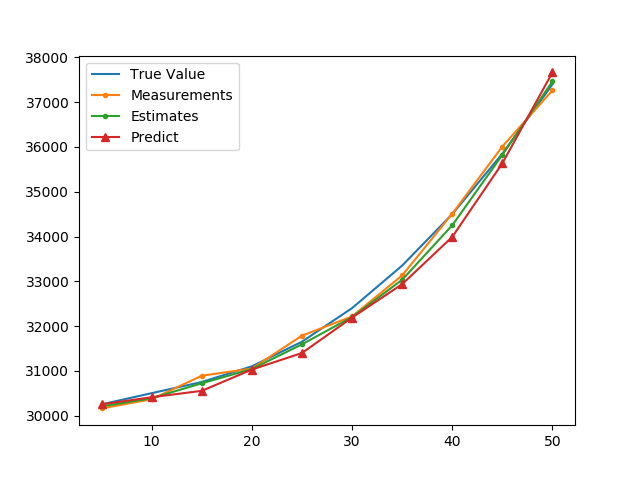
总结
$\alpha-\beta-(\gamma)$滤波器的种类有很多,基于相同的原理:
- 当前状态估计基于状态更新方程
- 状态的下一个估计值基于动态模型方程
常用的$\alpha-\beta-(\gamma)$滤波器:
- Wiener Filter 维纳滤波
- Beyes Filter 贝叶斯滤波
- Fading-memory polynomial Filter
- Expanding-memory (or growing-memory) polynomial Filter
- Least-squares Filter 最小二乘法滤波
- Benedict–Bordner Filter
- Lumped Filter
- Discounted least-squares $\alpha-\beta$ Filter
- Critically damped $\alpha-\beta$ Filter
- Growing-memory Filter
- Kalman Filter 卡尔曼滤波
- Extended Kalman Filter 扩展卡尔曼滤波
- Unscented Kalman Filter 无迹卡尔曼滤波
- Extended Complex Kalman Filter
- Gauss-Hermite Kalman Filter
- Cubature Kalman Filter
- Particle Filter 粒子滤波器
一维卡尔曼滤波
一维卡尔曼滤波不处理噪声
卡尔曼滤波基于5个方程,熟悉的有两个
- 状态更新方程
- 动态模型方程
下面会介绍卡尔曼滤波方程
在金条问题中,测量值和真实值的差异在于测量误差。由于测量误差是随机的,可以用方差$\sigma^2$表示,测量数据的方差可以通过天平供应商提供或者通过标定得到。方差代表测量不确定性(measurement uncertainty)或者(measurement error)
用$r$代表测量不确定性
估计值和真实值的误差为估计误差(estimate error)。当测量的次数越多时,估计误差越来越小,趋向于0。估计值也趋向于真实值。我们不知道估计误差是多少,但是可以估计估计不确定性(uncertainty in estimate)
用$p$表示估计不确定性
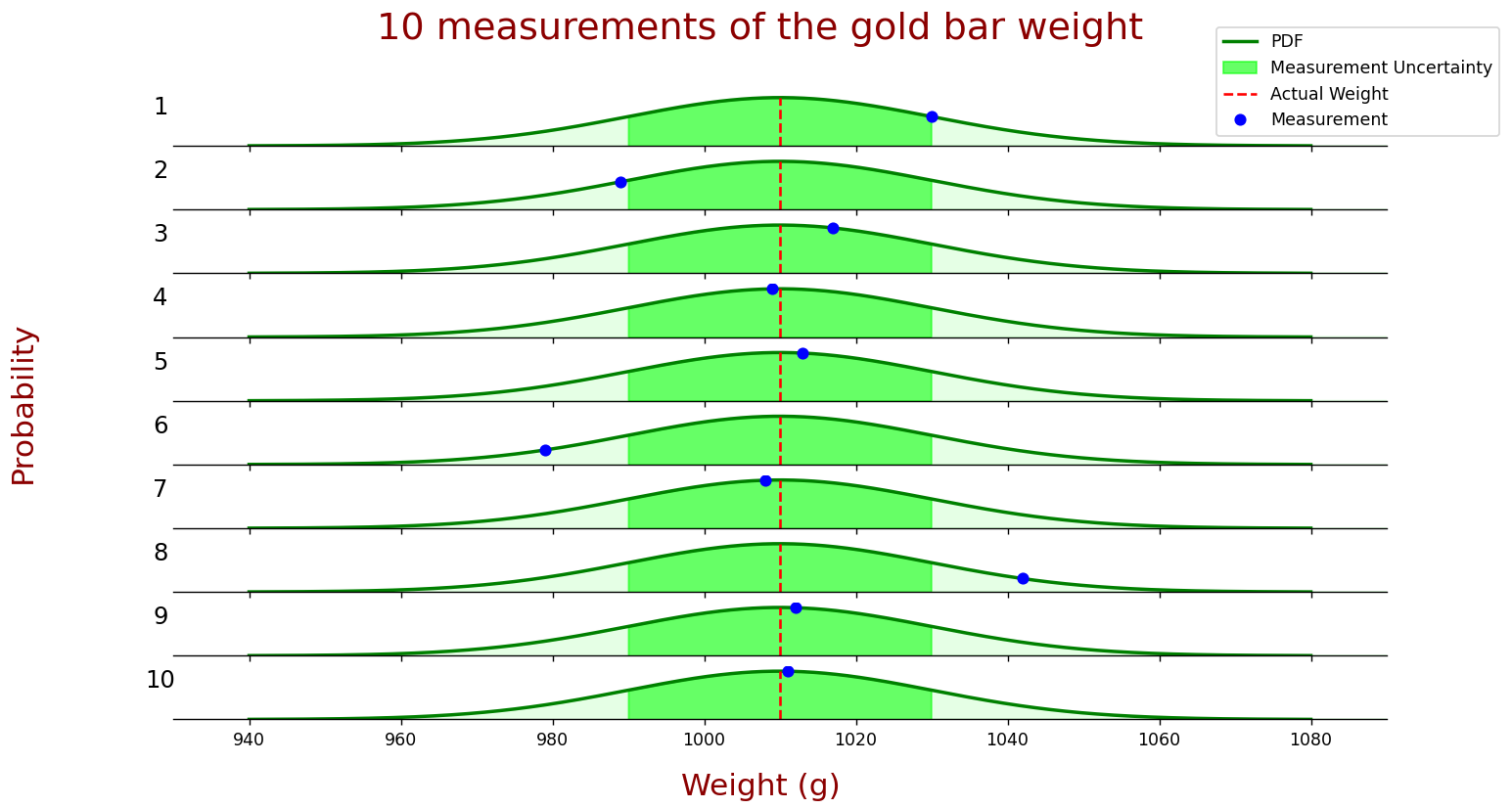
图中绿色区域代表标准差为$\sigma$的高斯分布下概率为68.26%的区域,$r=\sigma^2$
一维卡尔曼滤波增益方程
第三个方程为卡尔曼增益方程。在卡尔曼增益方程中,$\alpha-\beta(-\gamma)$每次迭代都动态的计算,这些参数用卡尔曼增益$K_n$表示,方程如下:
$$ K_n=\frac{估计不确定性}{估计不确定性+测量不确定性}=\frac{p_{n,n-1} }{p_{n,n-1}+r_n} $$$p_{n,n-1}$为外推估计不确定性,$r_n$为测量不确定性。
卡尔曼增益的取值范围为$0\leq K_n \leq 1$
重写状态更新方程:
$$ \hat{x}_{n,n}=\hat{x}_{n,n-1}+K_n(z_n-\hat{x}_{n,n-1})=(1-K_n)\hat{x}_{n,n-1}+K_n z_n $$当测量不确定性很大,估计不确定性很小时,卡尔曼增益接近0。估计占据很大权重而测量占据很小的权重
当测量不确定性很小,估计不确定性很大时,卡尔曼赠与接近1,估计占据很小权重而测量占据很大的权重
如果两张不确定性相等,则卡尔曼增益等于0.5
卡尔曼增益说明该根据测量值调整多少估计值
一维估计不确定性更新方程
第四个卡尔曼滤波方程
$$ p_{n,n}=(1-K_n)p_{n,n-1} $$该方程更新估计不确定性,称为协方差更新方程(Covariance Update Equation)
每次迭代$p$的值都会变小
一维外推估计不确定性
外推估计不确定性通过动态模型方程更新,在第2个例子中,
$$ \begin{array}{c} \hat{x}_{n+1,n}= \hat{x}_{n,n}+ \Delta t\hat{\dot{x} }_{n,n} \\ \hat{\dot{x} }_{n+1,n}= \hat{\dot{x} }_{n,n} \end{array} $$同样的对于外推估计不确定性,第五个卡尔曼滤波方程,协方差外推方程(Covariance Extrapolation Equation)
$$ \begin{array}{c} p_{n+1,n}^{x}= p_{n,n}^{x} + \Delta t^{2} \cdot p_{n,n}^{v} \\ p_{n+1,n}^{v}= p_{n,n}^{v} \end{array} $$其中$p^x$为位置估计不确定性,$p^v$为速度估计不确定性
放到一起
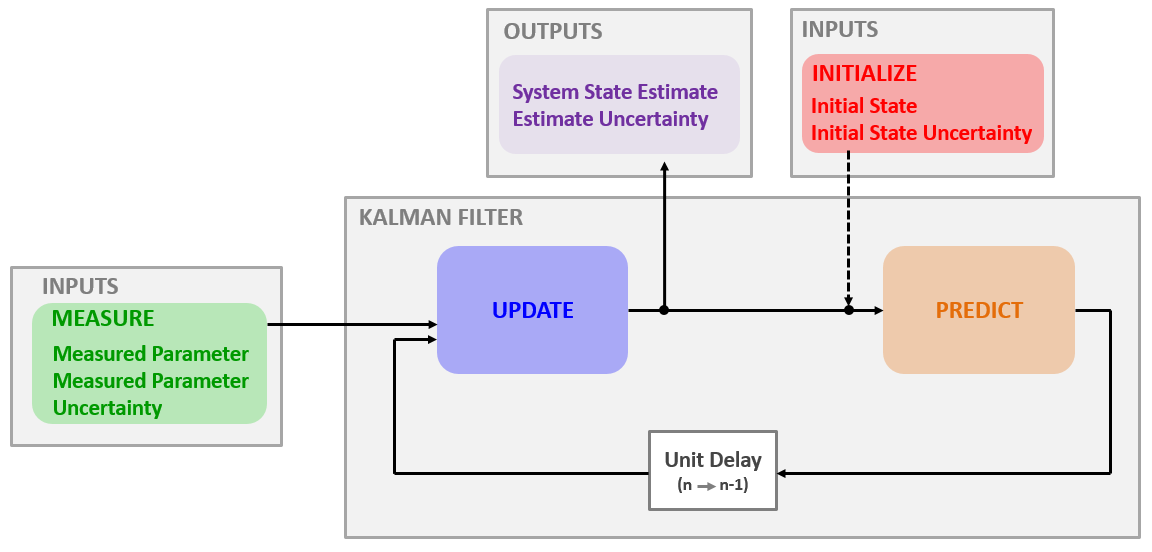
输入:
- 初始值
- 初始系统状态$(\hat{x}_{1,0})$
- 初始系统不确定性$(p_{1,0})$
- 测量值
- 测量系统状态$(z_n)$
- 测量系统不确定性$(r_n)$
测量系统不确定性由设备厂商提供,或者通过测量设备标定。雷达的测量不确定性取决SNR(信噪比),波束宽度,带宽,目标上的时间,时钟稳定性等等。每次雷达测量都会有不同的信噪比,波束宽度,目标上的时间。因此,雷达计算每次测量的不确定性,并将其报告给跟踪器。
滤波器的输出:
- 系统状态估计$(\hat{x}_{n,n})$
- 估计不确定性$(p_{n,n})$
除了系统状态估计,卡尔曼滤波器提供不确定性估计
$$ p_{n,n}=(1-K_n)p_{n,n-1} $$随着迭代的次数增加,$p_{n,n}$会越来越小
取多少测量值是取决于我们自己的,如果我们测量建筑的高度,对于精度在3厘米($\sigma$)感兴趣,我们将会在估计不确定性($\sigma^2$)小于9平方厘米是进行测量
总结卡尔曼滤波方程
| 方程 | 方程名称 | 其他叫法 |
|---|---|---|
| $\hat{x}_{n,n}=~ \hat{x}_{n,n-1}+ K_{n} \left( z_{n}- \hat{x}_{n,n-1} \right)$ | 状态更新 | 滤波方程 |
| $\hat{x}_{n+1,n}= \hat{x}_{n,n}+ \Delta t\hat{\dot{x} }_{n,n}$ $\hat{\dot{x} }_{n+1,n}= \hat{\dot{x} }_{n,n}$ (对于等速动态系统) |
状态外推 | 预测方程 转移方程 动态模型 状态空间模型 |
| $K_{n}= \frac{p_{n,n-1} }{p_{n,n-1}+r_{n} }$ | 卡尔曼增益 | 权重方程 |
| $p_{n,n}=~ \left( 1-K_{n} \right) p_{n,n-1}$ | 协方差更新 | 校正方程 |
| $p_{n+1,n}= p_{n,n}$ (对于常动态系统) |
协方差外推 | 预测协方差方程 |
状态外推方程和协方差外推方程取决于动态系统
以上代表特殊情况下的卡尔曼滤波方程。
卡尔曼滤波描述图
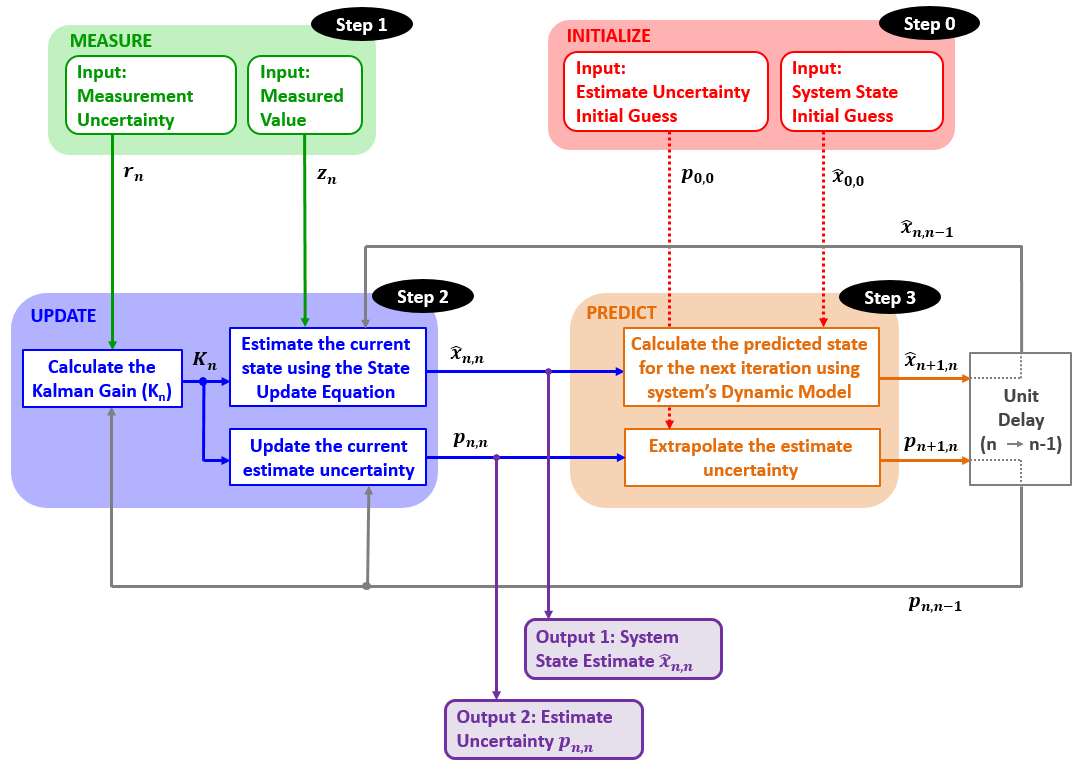
-
步骤0:初始化
- 初始化系统状态($\hat{x}_{1,0}$)
- 初始化状态不确定性($p_{1,0}$)
-
步骤1:测量
- 测量系统状态($z_n$)
- 测量不确定性($r_n$)
-
步骤2:状态更新
输入
- 测量值($z_{1,0}$)
- 测量不确定性($r_n$)
- 之前的系统状态估计($\hat{x}_{n,n-1}$)
- 估计不确定性($p_{n,n-1}$)
输出
- 当前系统状态估计($\hat{x}_{n,n}$)
- 当前状态估计不确定性($p_{n,n}$)
-
步骤3:预测
预测过程根据系统的动态模型,将当前系统状态和当前系统状态估计的不确定性推断到下一个系统状态。
在第一次滤波迭代时,初始化输出被视为前一状态估计和不确定性。
在接下来的滤波迭代中,预测输出成为上一状态估计和不确定性。
卡尔曼增益直观表现
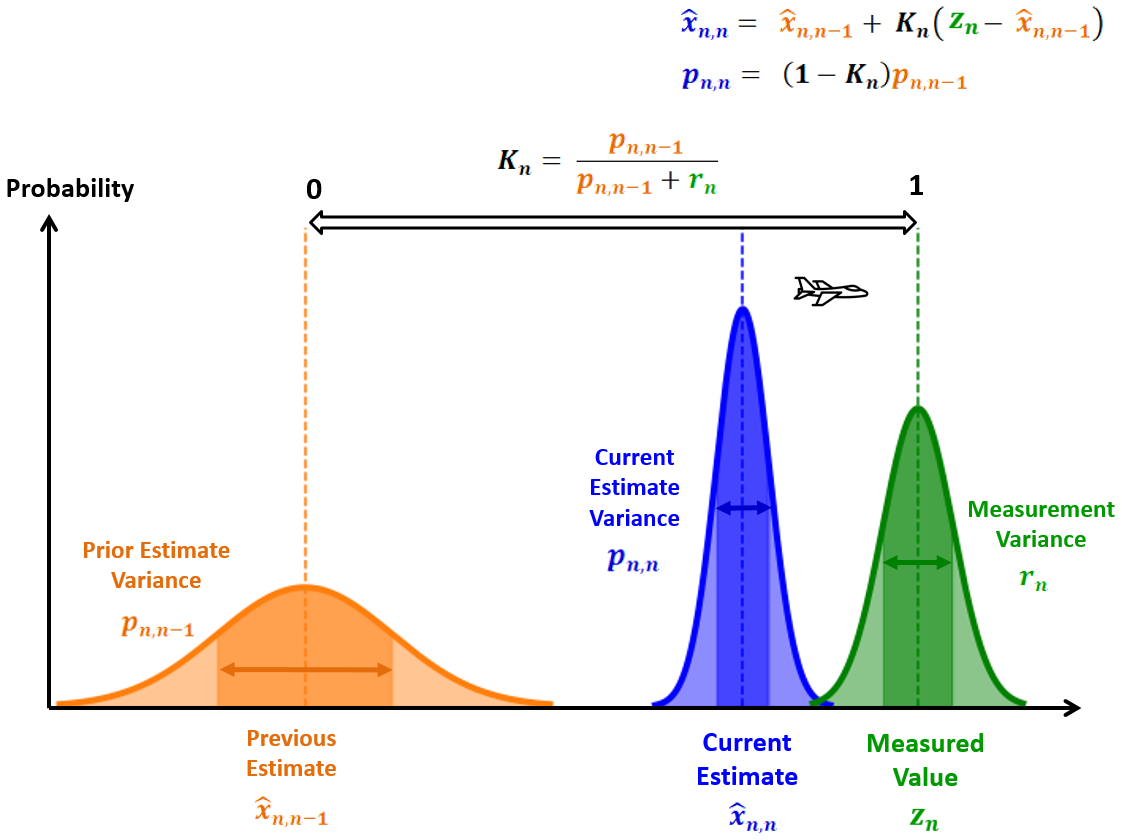
高卡尔曼增益
相对于估计不确定性的低测量不确定性将导致高卡尔曼增益(接近1)。这意味着新的估计值将接近于测量值。下图说明了在飞机跟踪应用中,高卡尔曼增益对估计的影响。
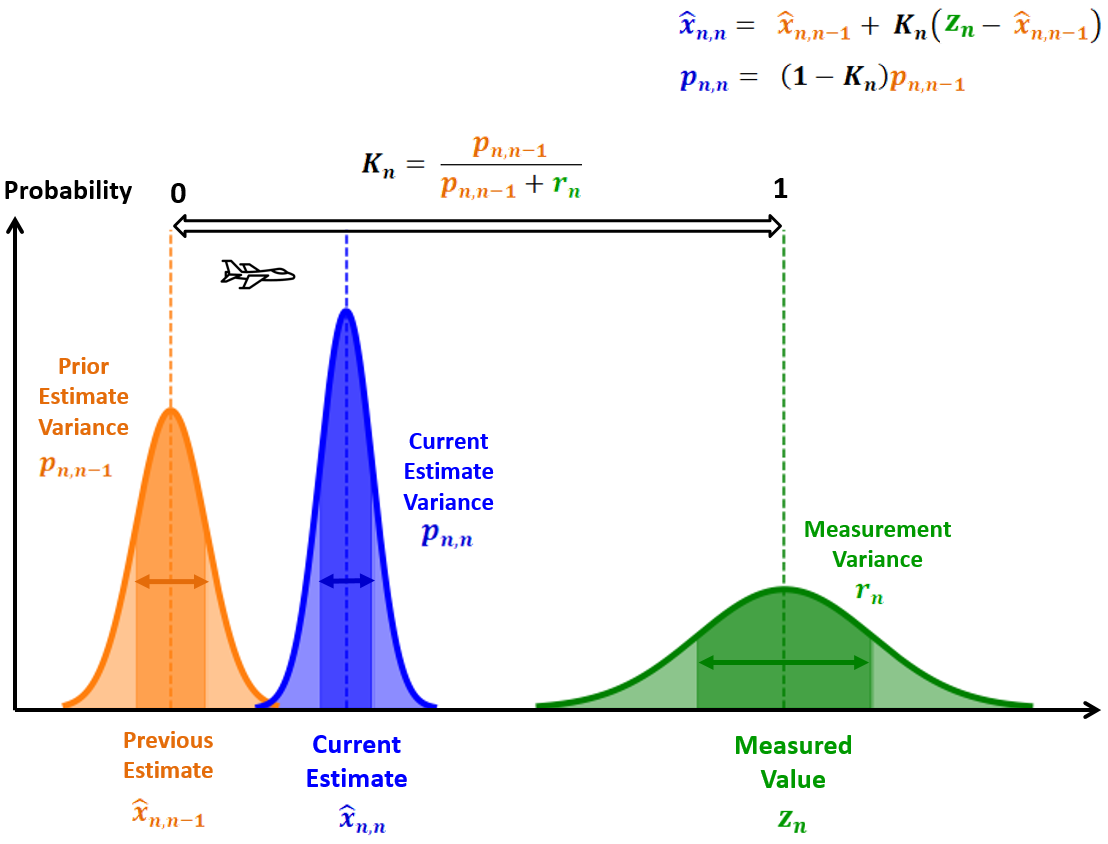
低卡尔曼增益
相对于估计不确定性的高测量不确定性将导致低卡尔曼增益(接近于0)。这意味着新的估计值将接近于先前的估计值。下图说明了在飞机跟踪应用中,低卡尔曼增益对估计的影响。
例子5-估计建筑物高度
数值信息:
- 真实高度50m
- 高度计误差(标准差)5m
- 测量值: 48.54m, 47.11m, 55.01m, 55.15m, 49.89m, 40.85m, 46.72m, 50.05m, 51.27m, 49.95m
代码
import matplotlib.pyplot as plt
measure = []
true = []
estimate = []
estimate_n = 60
predict = []
estimate_p = []
estimate_p_n = 15 * 15
measure_r_n = 5 * 5
gain = []
def kalman_filter():
global estimate_n, estimate_p_n
for i in range(0, len(measure)):
# 估计
gain_n = estimate_p_n / (estimate_p_n + measure_r_n)
gain.append(gain_n)
x = estimate_n + gain_n * (measure[i] - estimate_n)
p = (1 - gain_n) * estimate_p_n
# 保存
estimate.append(x)
estimate_p.append(p)
# 预测
estimate_n = x
estimate_p_n = p
true.append(50)
if __name__ == '__main__':
measure = [48.54, 47.11, 55.01, 55.15, 49.89, 40.85, 46.72, 50.05, 51.27, 49.95]
kalman_filter()
X = range(1, len(measure) + 1)
plt.figure()
plt.plot(X, true, label="True Value")
plt.plot(X, measure, label="Measurements", marker='.')
plt.plot(X, estimate, label="Estimates", marker='.')
plt.legend(loc='upper left')
plt.grid(True)
plt.figure()
plt.plot(X, gain, label="gain")
plt.legend(loc='upper right')
plt.grid(True)
plt.show()
结果
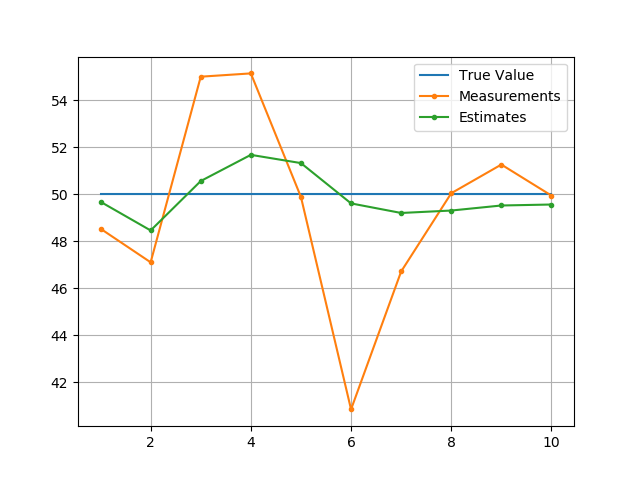
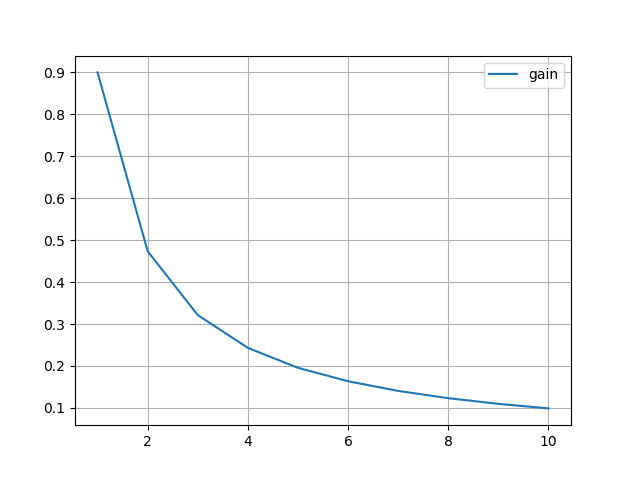
可以看到卡尔曼增益随着测量次数增加逐渐降低
一维卡尔曼滤波完整模型
处理噪声
真实世界中动态系统模型存在不确定性。例如当我们想估计电阻的电阻值时,我们假设一个恒定的动态模型,例如阻值在测量的时候不变。但是阻值会根据温度产生轻微的变化。用雷达跟踪弹道导弹时,动态模型的不确定性包括目标加速度的随机变化。对于飞机来说,由于可能的飞机机动性,不确定性要大得多。
另一方面,当我们使用GPS接收器估计一个静态物体的位置时,动态模型的不确定性为零,因为静态物体不移动。动态模型的不确定性被称为过程噪声(Process Noise)。在文献中,它也被称为工厂噪声、驱动噪声、动力学噪声、模型噪声和系统噪声。过程噪声产生估计误差。
在前面的例子中,我们估计了一个建筑物的高度。建筑物的高度并没有变化。因此,我们没有考虑到过程中的噪声。
过程噪声方差(Process Noise Variance)用$q$表示
协方差外推方程需要包含过程噪声方差
方程变为:
$$ p_{n+1,n}=p_{n,n}+q_n $$| 方程 | 方程名称 | 其他叫法 |
|---|---|---|
| $\hat{x}_{n,n}=~ \hat{x}_{n,n-1}+ K_{n} \left( z_{n}- \hat{x}_{n,n-1} \right)$ | 状态更新 | 滤波方程 |
| $\hat{x}_{n+1,n}= \hat{x}_{n,n}+ \Delta t\hat{\dot{x} }_{n,n}$ $\hat{\dot{x} }_{n+1,n}= \hat{\dot{x} }_{n,n}$ (对于等速动态系统) |
状态外推 | 预测方程 转移方程 动态模型 状态空间模型 |
| $K_{n}= \frac{p_{n,n-1} }{p_{n,n-1}+r_{n} }$ | 卡尔曼增益 | 权重方程 |
| $p_{n,n}=~ \left( 1-K_{n} \right) p_{n,n-1}$ | 协方差更新 | 校正方程 |
| $p_{n+1,n}= p_{n,n}+q_n$ (对于常动态系统) |
协方差外推 | 预测协方差方程 |
例子6-估计箱体里面液体的温度
假设液体的温度是恒定的,而真正的系统温度存在一点波动,方程为:
$$ x_n=T+w_n $$$T$为常温度,$w_n$为随机噪声,其方差为$q$
数值信息:
- 真实温度为50℃
- 过程噪声方差为0.0001
- 测量标准差为0.1℃
- 测量间隔5s
- 真实数据为:49.979℃, 50.025℃, 50℃, 50.003℃, 49.994℃, 50.002℃, 49.999℃, 50.006℃, 49.998℃, 49.991℃
- 测量数据为:49.95℃, 49.967℃, 50.1℃, 50.106℃, 49.992℃, 49.819℃, 49.933℃, 50.007℃, 50.023℃, 49.99℃
对比
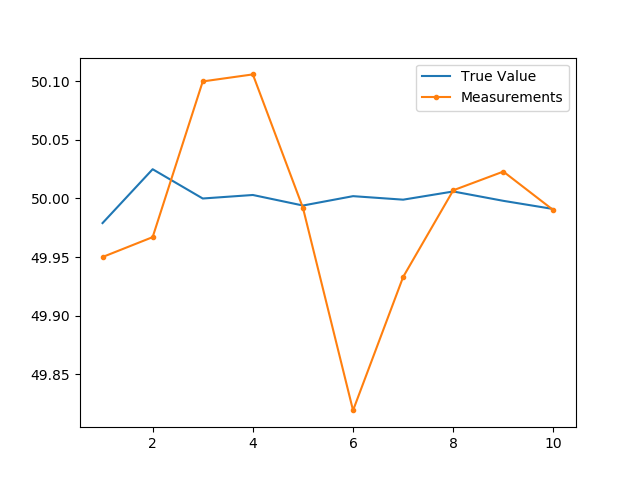
代码
import matplotlib.pyplot as plt
measure = []
true = []
estimate = []
estimate_n = 10
predict = []
estimate_p = []
estimate_p_n = 100 * 100
measure_r_n = 0.1 * 0.1
gain = []
q = 0.0001
def kalman_filter():
global estimate_n, estimate_p_n
for i in range(0, len(measure)):
# 估计
gain_n = estimate_p_n / (estimate_p_n + measure_r_n)
gain.append(gain_n)
x = estimate_n + gain_n * (measure[i] - estimate_n)
p = (1 - gain_n) * estimate_p_n
# 保存
estimate.append(x)
estimate_p.append(p)
# 预测
estimate_n = x
estimate_p_n = p + q
if __name__ == '__main__':
true = [49.979, 50.025, 50, 50.003, 49.994, 50.002, 49.999, 50.006, 49.998, 49.991]
measure = [49.95, 49.967, 50.1, 50.106, 49.992, 49.819, 49.933, 50.007, 50.023, 49.99]
kalman_filter()
X = range(1, len(measure) + 1)
plt.figure()
plt.plot(X, true, label="True Value")
plt.plot(X, measure, label="Measurements", marker='.')
plt.plot(X, estimate, label="Estimates", marker='.')
plt.legend(loc='upper right')
plt.grid(True)
plt.figure()
plt.plot(X, gain, label="gain")
plt.legend(loc='upper right')
plt.grid(True)
plt.show()
结果:
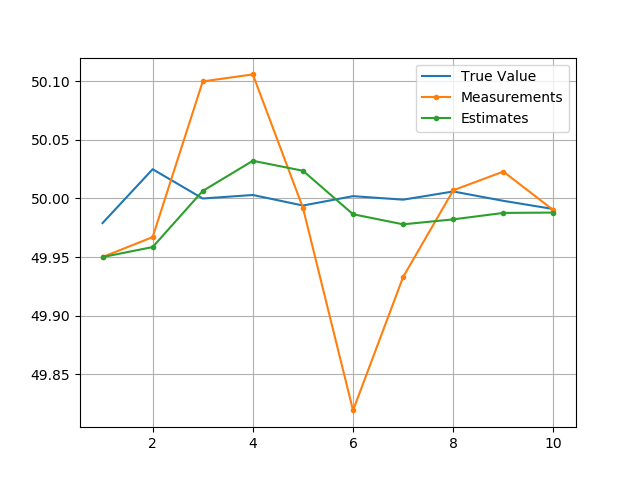
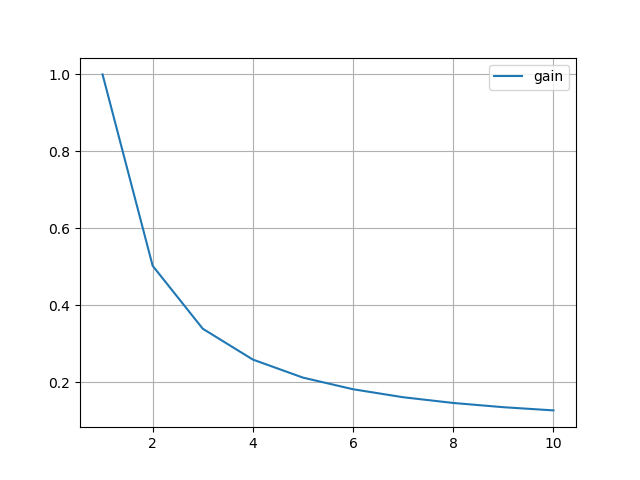
例子7-估计加热液体的温度Ⅰ
数值信息:
- 过程噪声方差0.0001
- 测量误差标准差0.1℃
- 测量间隔5s
- 系统的动态是恒定的
- 真实温度:50.479℃, 51.025℃, 51.5℃, 52.003℃, 52.494℃, 53.002℃, 53.499℃, 54.006℃, 54.498℃, 54.991℃
- 测量温度:50.45℃, 50.967℃, 51.6℃, 52.106℃, 52.492℃, 52.819℃, 53.433℃, 54.007℃, 54.523℃, 54.99℃
代码
import matplotlib.pyplot as plt
measure = []
true = []
estimate = []
estimate_n = 10
predict = []
estimate_p = []
estimate_p_n = 100 * 100
measure_r_n = 0.1 * 0.1
gain = []
q = 0.0001
def kalman_filter():
global estimate_n, estimate_p_n
for i in range(0, len(measure)):
# 估计
gain_n = estimate_p_n / (estimate_p_n + measure_r_n)
gain.append(gain_n)
x = estimate_n + gain_n * (measure[i] - estimate_n)
p = (1 - gain_n) * estimate_p_n
# 保存
estimate.append(x)
estimate_p.append(p)
# 预测
estimate_n = x
estimate_p_n = p + q
if __name__ == '__main__':
true = [50.479, 51.025, 51.5, 52.003, 52.494, 53.002, 53.499, 54.006, 54.498, 54.991]
measure = [50.45, 50.967, 51.6, 52.106, 52.492, 52.819, 53.433, 54.007, 54.523, 54.99]
kalman_filter()
X = range(1, len(measure) + 1)
plt.figure()
plt.plot(X, true, label="True Value")
plt.plot(X, measure, label="Measurements", marker='.')
plt.plot(X, estimate, label="Estimates", marker='.')
plt.legend(loc='upper right')
plt.grid(True)
plt.figure()
plt.plot(X, gain, label="gain")
plt.legend(loc='upper right')
plt.grid(True)
plt.show()
结果
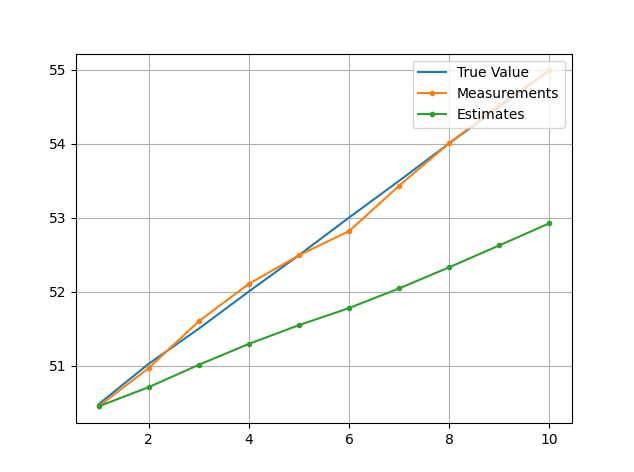
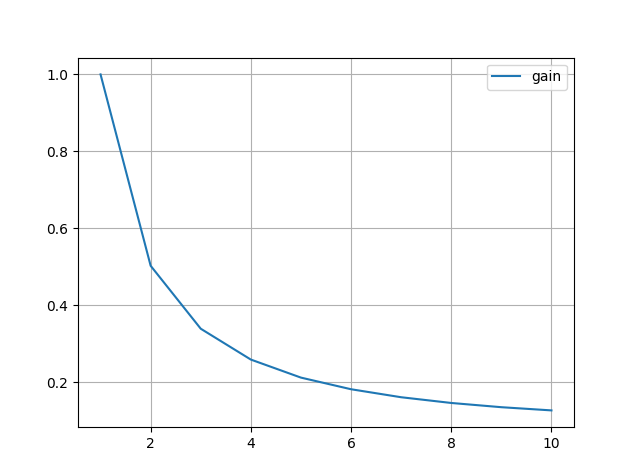
总结
在这个例子中,我们用一个具有恒定动态模型的一维卡尔曼滤波器测量加热液体的温度。我们观察到卡尔曼滤波估计中的滞后误差。滞后误差是由错误的动态模型定义和错误的过程模型定义造成的。
滞后误差可以通过对动态模型或过程模型的适当定义来解决。
例子8-估计加热液体的温度Ⅱ
把过程不确定性调整为0.15
相同的代码得到结果
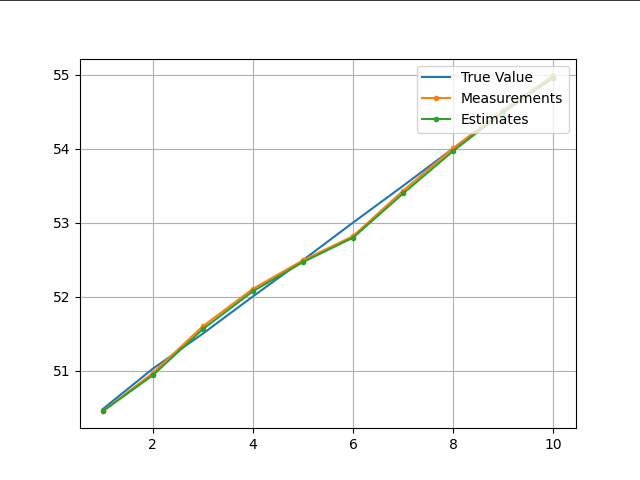
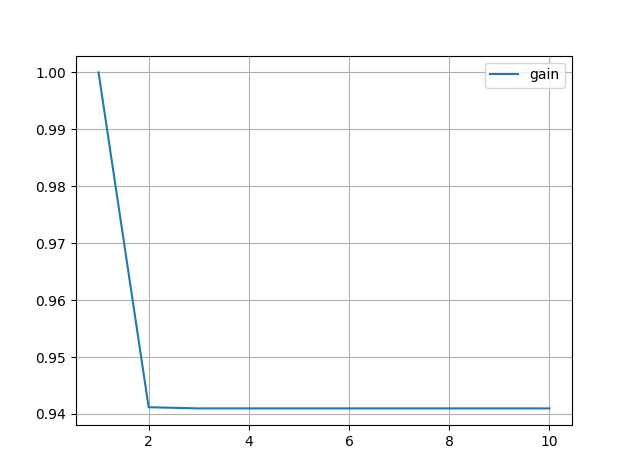
从图上看,估计值和测量值几乎重合,而且卡尔曼增益没有收敛于0,模型定义是存在问题的
总结
我们可以通过设置一个高的过程不确定性来摆脱滞后误差。然而,由于我们的模型没有很好地定义,我们得到的是几乎等于测量值的噪声估计值,而我们错过了卡尔曼滤波的目标。
最好的卡尔曼滤波器的实施将涉及一个非常接近现实的模型,为过程噪声留下一点空间。然而,一个精确的模型并不总是可用的–例如,飞机驾驶员可能决定执行一个突然的机动动作,这将改变预测的飞机轨迹。在这种情况下,过程噪声就会增加。
多维卡尔曼滤波
前言
很多场景下动态过程有两个甚至多个维度,例如描述飞机位置的空间有3个维度
$$ \begin{bmatrix} x\\ y\\ z \end{bmatrix} $$描述飞机位置和速度有6个维度
$$ \begin{bmatrix} x\\ y\\ z\\ \dot{x}\\ \dot{y}\\ \dot{z} \end{bmatrix} $$描述飞机位置、速度和加速度有9个维度
$$ \begin{bmatrix} x\\ y\\ z\\ \dot{x}\\ \dot{y}\\ \dot{z}\\ \ddot{x}\\ \ddot{y}\\ \ddot{z} \end{bmatrix} $$假设常加速度模型,外推飞机状态方程如下:
$$ \begin{cases} x_{n} = x_{n-1} + \dot{x}_{n-1} \Delta t+ \frac{1}{2}\ddot{x}_{n-1} \Delta t^{2}\\ y_{n} = y_{n-1} + \dot{y}_{n-1} \Delta t+ \frac{1}{2}\ddot{y}_{n-1} \Delta t^{2}\\ z_{n} = z_{n-1} + \dot{z}_{n-1} \Delta t+ \frac{1}{2}\ddot{z}_{n-1} \Delta t^{2}\\ \dot{x}_{n} = \dot{x}_{n-1} + \ddot{x}_{n-1} \Delta t\\ \dot{y}_{n} = \dot{y}_{n-1} + \ddot{y}_{n-1} \Delta t\\ \dot{z}_{n} = \dot{z}_{n-1} + \ddot{z}_{n-1} \Delta t\\ \ddot{x}_{n} = \ddot{x}_{n-1}\\ \ddot{y}_{n} = \ddot{y}_{n-1}\\ \ddot{z}_{n} = \ddot{z}_{n-1}\\ \end{cases} $$用矩阵形式的单一方程来描述一个多维过程是常见的做法。
首先,写所有这些方程是非常累人的;用矩阵符号表示它们要短得多,也更优雅。
其次,计算机在矩阵计算方面非常高效。以矩阵形式实现卡尔曼滤波,可以获得更快的计算运行时间。
准备知识
参考
- 矩阵运算
- 加法乘法
- 转置
- 逆矩阵
- 对称矩阵
- 协方差和协方差矩阵
协方差和协方差矩阵
协方差定义
$$ \operatorname{cov}(X,Y)=\operatorname{E}[(X-\operatorname{E}[X])(Y-\operatorname{E}[Y])] $$相关系数:
$$ \rho=\frac{\operatorname{cov}(X,Y)}{\sigma_X\sigma_Y} $$样本协方差:
$$ \operatorname{cov}(X,Y)=\frac{\sum_{i=1}^n{(x_i-\overline x)(y_i-\overline y)} }{n-1} $$分母为$n-1$才能做到无偏估计
协方差矩阵:
$$ \operatorname{K}_{\mathbf{X}\mathbf{X} }= \begin{bmatrix} \mathrm{E}[(X_1 - \operatorname{E}[X_1])(X_1 - \operatorname{E}[X_1])] & \mathrm{E}[(X_1 - \operatorname{E}[X_1])(X_2 - \operatorname{E}[X_2])] & \cdots & \mathrm{E}[(X_1 - \operatorname{E}[X_1])(X_n - \operatorname{E}[X_n])] \\ \\ \mathrm{E}[(X_2 - \operatorname{E}[X_2])(X_1 - \operatorname{E}[X_1])] & \mathrm{E}[(X_2 - \operatorname{E}[X_2])(X_2 - \operatorname{E}[X_2])] & \cdots & \mathrm{E}[(X_2 - \operatorname{E}[X_2])(X_n - \operatorname{E}[X_n])] \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \mathrm{E}[(X_n - \operatorname{E}[X_n])(X_1 - \operatorname{E}[X_1])] & \mathrm{E}[(X_n - \operatorname{E}[X_n])(X_2 - \operatorname{E}[X_2])] & \cdots & \mathrm{E}[(X_n - \operatorname{E}[X_n])(X_n - \operatorname{E}[X_n])] \end{bmatrix} $$例子:
$$ Z=\begin{bmatrix} 1 & 2 \\ 3 & 6 \\ 4 & 2 \\ 5 & 2 \end{bmatrix} $$$$ X=\begin{bmatrix} 1 \\ 3 \\ 4 \\ 5 \end{bmatrix}, \quad Y=\begin{bmatrix} 2 \\ 6 \\ 2 \\ 2 \end{bmatrix} $$$$ \operatorname{cov}(Z)=\begin{bmatrix} \operatorname{cov}(X,X) & \operatorname{cov}(X,Y) \\ \operatorname{cov}(Y,X) & \operatorname{cov}(Y,Y) \end{bmatrix} $$计算过程
$$ \begin{align} \operatorname{cov}(X,X)=&\frac{(1-3.25)^2+(3-3.25)^2+(4-3.25)^2+(5-3.25)^2}{4-1}=2.9167\\ \operatorname{cov}(X,Y)=&\frac{(1-3.25)(2-3)+(3-3.25)(6-3)+(4-3.25)(2-3)+(5-3.25)(2-3)}{4-1}=-0.3333\\ \operatorname{cov}(Y,X)=&\frac{(2-3)(1-3.25)+(6-3)(3-3.25)+(2-3)(4-3.25)+(2-3)(5-3.25)}{4-1}=-0.3333\\ \operatorname{cov}(Y,Y)=&\frac{(2-3)^2+(6-3)^2+(2-3)^2+(2-3)^2}{4-1}=4 \end{align} $$$$ \operatorname{cov}(Z)=\begin{bmatrix} 2.9167 & -0.3333 \\ -0.3333 & 4.000 \end{bmatrix} $$Python测试代码:
import numpy as np
Z = np.array([1,2,3,6,4,2,5,2]).reshape((4,2))
print(np.cov(Z, rowvar=False)) #设置列向量为一个个的变量其他参考
https://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/
期望代数
$$ E(X)=\mu_X $$$\mu_X$为随机数的均值
基本规则
| 规则 | 笔记 | |
|---|---|---|
| 1 | $E(X)=\mu_X=\sum xp(x)$ | $p(x)$为$x$的离散概率 |
| 2 | $E(a)=a$ | $a$为常数 |
| 3 | $E(aX)=aE(X)$ | $a$为常数 |
| 4 | $E(a\pm X)=a\pm E(X)$ | $a$为常数 |
| 5 | $E(a\pm bX)=a\pm bE(X)$ | $a,b$为常数 |
| 6 | $E(X\pm Y)=E(X)\pm E(Y)$ | $Y$为另一个随机变量 |
| 7 | $E(XY)=E(X)E(Y)$ | 如果$X,Y$互不相关 |
方差和协方差规则
| 规则 | 笔记 | |
|---|---|---|
| 8 | $V(a)=0$ | $V(a)$是$a$的方差,$a$为常数 |
| 9 | $V(a\pm X)=V(X)$ | $V(X)$为$X$的方差,$a$为常数 |
| 10 | $V(X)=E(X^2)-\mu^2_X$ | $V(X)$为$X$的方差 |
| 11 | $COV(X,Y)=E(XY)-\mu_X\mu_Y$ | $COV(X,Y)$为$X$和$Y$的协方差 |
| 12 | $COV(X,Y)=0$ | 如果$X$和$Y$相互独立 |
| 13 | $V(aX)=a^2V(X)$ | $a$为常数 |
| 14 | $V(X\pm Y)=V(X)+V(Y)\pm 2COV(X,Y)$ | |
| 15 | $V(XY)\neq V(X)V(Y)$ |
规则10论证:
$$ V(X) = E(X^{2}) - \mu_{X}^{2} $$| 笔记 | |
|---|---|
| $V(X) = \sigma_{X}^2 = E((X - \mu_{X})^2) =$ | |
| $E(X^2 -2X\mu_{X} + \mu_{X}^2) =$ | |
| $E(X^2) - E(2X\mu_{X}) + E(\mu_{X}^2) =$ | 使用规则5 |
| $E(X^2) - 2\mu_{X}E(X) + E(\mu_{X}^2) =$ | 使用规则3 |
| $E(X^2) - 2\mu_{X}E(X) + \mu_{X}^2 =$ | 使用规则2 |
| $E(X^2) - 2\mu_{X}\mu_{X} + \mu_{X}^2 =$ | 使用规则1 |
| $E(X^2) - \mu_{X}^2$ |
规则11论证:
$$ COV(X,Y) = E(XY) - \mu_{X}\mu_{Y} $$| 笔记 | |
|---|---|
| $COV(X,Y) = E((X - \mu_{X})(Y - \mu_{Y}))$ | |
| $E(XY - X \mu_{Y} - Y \mu_{X} + \mu_{X}\mu_{Y}) =$ | |
| $E(XY) - E(X \mu_{Y}) - E(Y \mu_{X}) + E(\mu_{X}\mu_{Y}) =$ | 使用规则6 |
| $E(XY) - \mu_{Y} E(X) - \mu_{X} E(Y) + E(\mu_{X}\mu_{Y}) =$ | 使用规则3 |
| $E(XY) - \mu_{Y} E(X) - \mu_{X} E(Y) + E(\mu_{X}\mu_{Y}) =$ | 使用规则2 |
| $E(XY) - \mu_{Y} \mu_{X} - \mu_{X} \mu_{Y} + \mu_{X}\mu_{Y} =$ | 使用规则1 |
| $E(XY) - \mu_{X}\mu_{Y}$ |
协方差矩阵与期望
假设向量$x$有$k$个元素
$$ \boldsymbol{x} = \begin{bmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{k}\\ \end{bmatrix} $$$x$的协方差矩阵定义为
$$ COV(\boldsymbol{x})= E\left(\left(\boldsymbol{x - \mu_{x} }\right)\left(\boldsymbol{x - \mu_{x} }\right)^{T}\right) $$证明:
$$ \begin{align} COV(\boldsymbol{x}) =& E\left( \begin{bmatrix} (x_1 - \mu_{x_1})^2 & (x_1 - \mu_{x_1})(x_2 - \mu_{x_2}) & \cdots & (x_1 - \mu_{x_1})(x_k - \mu_{x_k}) \\ (x_2 - \mu_{x_2})(x_1- \mu_{x_1}) & (x_2 - \mu_{x_2})^2 & \cdots & (x_2 - \mu_{x_2})(x_k - \mu_{x_k}) \\ \vdots & \vdots & \ddots & \vdots \\ (x_k - \mu_{x_k})(x_1 - \mu_{x_1}) & (x_k - \mu_{x_k})(x_2 - \mu_{x_2}) & \cdots & (x_k - \mu_{x_k})^2 \\ \end{bmatrix}\right)\\= &E \left( \begin{bmatrix} (x_1 - \mu_{x_1}) \\ (x_2 - \mu_{x_2}) \\ \vdots \\ (x_k - \mu_{x_k}) \\ \end{bmatrix} \begin{bmatrix} (x_1 - \mu_{x_1}) & (x_{2} - \mu_{x_2}) & \cdots & (x_k - \mu_{x_k}) \end{bmatrix} \right)\\ = &E\left(\left(\boldsymbol{x - \mu_x}\right)\left(\boldsymbol{x - \mu_x}\right)^T\right) \end{align} $$状态外推方程
表示:
- 黑色小写字母代表向量
- 黑色大写字母代表矩阵
- 普通小写字母代表标量或者向量元素
- 普通大写字母代表矩阵元素
使用状态外推方程,我们可以根据对当前状态的了解,预测下一个系统状态。它将状态向量从现在(时间步数n)推断到未来(时间步数n+1)。
也叫作
- 预测方程
- 过渡方程
- 预测方程
- 动态模型
- 状态空间模型
一般形式
矩阵式的状态外推方程的一般形式是:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_n+w_n} $$其中: $\boldsymbol{\hat{x}_{n+1,n} }$ 为时间为$n+1$时预测系统状态向量 $\boldsymbol{\hat{x}_{n,n} }$ 为时间为$n$时系统状态向量 $\boldsymbol{u_n}$ 为控制变量或者输入变量-对系统的可测量的(确定性的)输入 $\boldsymbol{w_n}$ 为过程噪声或干扰–影响状态的不可测量的输入 $\boldsymbol{F}$ 为系统转移矩阵 $\boldsymbol{G}$ 为控制矩阵或输入转换矩阵(将控制变量映射到状态变量)
书面形式,状态转移矩阵$\boldsymbol F$有时候用$\boldsymbol \Phi$表示
描述
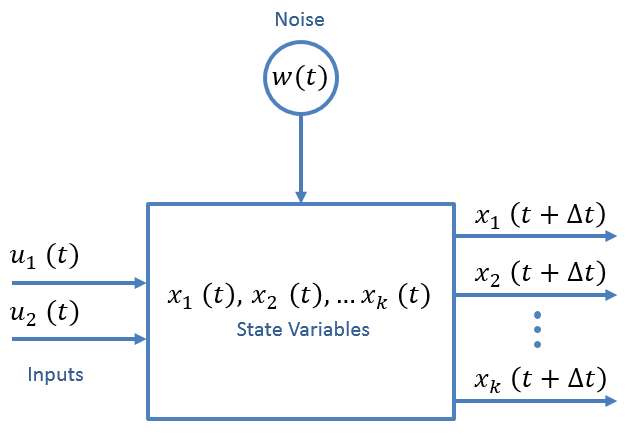
状态变量代表能够了解系统的参数
比如运动的飞机有位置、速度和加速度
需要知道哪些是系统变量,哪些是输入变量
- 移动的机械系统具有如下属性:位置、速度、加速度、阻力
- 作用于系统的力应被视为外部强制函数,即对系统的输入,控制状态矢量(恒定加速度情况下的位置和速度)
- 牛顿第二定律$F=ma$,可以考虑加速度是额外的系统输入
- 位置和速度是首要感兴趣的系统变量
例子-飞机-无控制输入
假设无控制输入
$$ \boldsymbol u_n=0 $$飞机以恒定加速度飞行,状态向量$\hat{\boldsymbol x}_n$为:
$$ \boldsymbol{\hat{x}_{n} }= \begin{bmatrix} \hat{x}_{n}\\ \hat{y}_{n}\\ \hat{z}_{n}\\ \hat{\dot{x} }_{n}\\ \hat{\dot{y} }_{n}\\ \hat{\dot{z} }_{n}\\ \hat{\ddot{x} }_{n}\\ \hat{\ddot{y} }_{n}\\ \hat{\ddot{z} }_{n}\\ \end{bmatrix} $$状态转移矩阵$\boldsymbol F$为:
$$ \boldsymbol{F}= \begin{bmatrix} 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2} & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2} & 0 \\ 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2}\\ 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ \end{bmatrix} $$状态外推方程为:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_n} $$$$ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{y}_{n+1,n}\\ \hat{z}_{n+1,n}\\ \hat{\dot{x} }_{n+1,n}\\ \hat{\dot{y} }_{n+1,n}\\ \hat{\dot{z} }_{n+1,n}\\ \hat{\ddot{x} }_{n+1,n}\\ \hat{\ddot{y} }_{n+1,n}\\ \hat{\ddot{z} }_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2} & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2} & 0 \\ 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & 0.5\Delta t^{2}\\ 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{y}_{n,n}\\ \hat{z}_{n,n}\\ \hat{\dot{x} }_{n,n}\\ \hat{\dot{y} }_{n,n}\\ \hat{\dot{z} }_{n,n}\\ \hat{\ddot{x} }_{n,n}\\ \hat{\ddot{y} }_{n,n}\\ \hat{\ddot{z} }_{n,n}\\ \end{matrix} \right] $$结果:
$$ \begin{cases} \hat{x}_{n+1,n} = \hat{x}_{n,n} + \hat{\dot{x} }_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{x} }_{n,n} \Delta t^{2}\\ \hat{y}_{n+1,n} = \hat{y}_{n,n} + \hat{\dot{y} }_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{y} }_{n,n} \Delta t^{2}\\ \hat{z}_{n+1,n} = \hat{z}_{n,n} + \hat{\dot{z} }_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{z} }_{n,n} \Delta t^{2}\\ \hat{\dot{x} }_{n+1,n} = \hat{\dot{x} }_{n,n} + \hat{\ddot{x} }_{n,n} \Delta t\\ \hat{\dot{y} }_{n+1,n} = \hat{\dot{y} }_{n,n} + \hat{\ddot{y} }_{n,n} \Delta t\\ \hat{\dot{z} }_{n+1,n} = \hat{\dot{z} }_{n,n} + \hat{\ddot{z} }_{n,n} \Delta t\\ \hat{\ddot{x} }_{n+1,n} = \hat{\ddot{x} }_{n,n}\\ \hat{\ddot{y} }_{n+1,n} = \hat{\ddot{y} }_{n,n}\\ \hat{\ddot{z} }_{n+1,n} = \hat{\ddot{z} }_{n,n}\\ \end{cases} $$例子-飞机-有控制输入
带控制输入,状态向量$\hat{\boldsymbol x}_n$为:
$$ \boldsymbol{\hat x}_{n}= \begin{bmatrix} \hat{x}_{n}\\ \hat{y}_{n}\\ \hat{z}_{n}\\ \hat{\dot{x} }_{n}\\ \hat{\dot{y} }_{n}\\ \hat{\dot{z} }_{n} \end{bmatrix} $$控制向量$\boldsymbol{u}_n$为笛卡尔坐标系中的飞机加速度:
$$ \boldsymbol u_n= \begin{bmatrix} \hat{\ddot{x} }_{n}\\ \hat{\ddot{y} }_{n}\\ \hat{\ddot{z} }_{n} \end{bmatrix} $$状态转移矩阵为:
$$ \boldsymbol{F}= \left[ \begin{matrix} 1 & 0 & 0 & \Delta t & 0 & 0\\ 0 & 1 & 0 & 0 & \Delta t & 0\\ 0 & 0 & 1 & 0 & 0 & \Delta t\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] $$控制矩阵为:
$$ \boldsymbol{G}= \left[ \begin{matrix} 0.5\Delta t^{2} & 0 & 0 \\ 0 & 0.5\Delta t^{2} & 0 \\ 0 & 0 & 0.5\Delta t^{2} \\ \Delta t & 0 & 0 \\ 0 & \Delta t & 0 \\ 0 & 0 & \Delta t \\ \end{matrix} \right] $$状态外推方程为:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_{n,n} } $$$$ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{y}_{n+1,n}\\ \hat{z}_{n+1,n}\\ \hat{\dot{x} }_{n+1,n}\\ \hat{\dot{y} }_{n+1,n}\\ \hat{\dot{z} }_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 & 0 & \Delta t & 0 & 0\\ 0 & 1 & 0 & 0 & \Delta t & 0\\ 0 & 0 & 1 & 0 & 0 & \Delta t\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{y}_{n,n}\\ \hat{z}_{n,n}\\ \hat{\dot{x} }_{n,n}\\ \hat{\dot{y} }_{n,n}\\ \hat{\dot{z} }_{n,n}\\ \end{matrix} \right] + \left[ \begin{matrix} 0.5\Delta t^{2} & 0 & 0 \\ 0 & 0.5\Delta t^{2} & 0 \\ 0 & 0 & 0.5\Delta t^{2} \\ \Delta t & 0 & 0 \\ 0 & \Delta t & 0 \\ 0 & 0 & \Delta t \\ \end{matrix} \right] \left[ \begin{matrix} \ddot{x}_{n}\\ \ddot{y}_{n}\\ \ddot{z}_{n}\\ \end{matrix} \right] $$例子-物体掉落
掉落物体的状态向量包含高度和速度:
$$ \boldsymbol {\hat x}_n=\begin{bmatrix} \hat h_n\\ \hat{\dot{h} }_n\\ \end{bmatrix} $$状态转移矩阵为:
$$ \boldsymbol{F}= \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] $$控制矩阵为:
$$ \boldsymbol{G}= \left[ \begin{matrix} 0.5\Delta t^{2} \\ \Delta t \\ \end{matrix} \right] $$输入变量为:
$$ \boldsymbol{u_{n} }= \left[ \begin{matrix} g \end{matrix} \right] $$$g$为重力加速度
状态外推方程为:
$$ \left[ \begin{matrix} \hat{h}_{n+1,n}\\ \hat{\dot{h} }_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \hat{h}_{n,n}\\ \hat{\dot{h} }_{n,n}\\ \end{matrix} \right] + \left[ \begin{matrix} 0.5\Delta t^{2} \\ \Delta t \\ \end{matrix} \right] \left[ \begin{matrix} g \end{matrix} \right] $$乘积结果:
$$ \begin{cases} \hat{h}_{n+1,n} = \hat{h}_{n,n} + \hat{\dot{h} }_{n,n} \Delta t + 0.5 \Delta t^{2} g\\ \hat{\dot{h} }_{n+1,n} = \hat{\dot{h} }_{n,n} + \Delta t g\\ \end{cases} $$状态外推方程维度
| 变量 | 描述 | 维度 |
|---|---|---|
| $\boldsymbol{x}$ | 状态向量 | $n_x \times 1$ |
| $\boldsymbol{F}$ | 状态转移矩阵 | $n_{x} \times n_x$ |
| $\boldsymbol{u}$ | 输入变量 | $n_{x} \times 1$ |
| $\boldsymbol{G}$ | 控制矩阵 | $n_{x} \times n_u$ |
| $\boldsymbol{w}$ | 过程噪声向量 | $n_{x} \times 1$ |
线性时不变系统
到目前为止讨论的都是现行时不变系统,LTI (Linear Time-Invariant)。用于具有时变动态的系统的卡尔曼滤波和用于非线性系统的卡尔曼滤波(扩展卡尔曼滤波)将在后面讨论
线性系统:线性系统是方程组,其中的变量从不相互相乘,只与常数相乘,然后相加。线性系统被用来描述变量之间的静态和动态关系。
线性系统的输出函数$\mathcal{F}$满足以下方程:
$$ \mathcal{F}(a\times g(t) + b\times h(t))=a\times\mathcal{F}(g(t))+b\times\mathcal{F}(h(t)) $$其中:
$a,b$都是常实数 $g,h$是独立于变量$t$的任意函数
一个时间不变的系统有一个系统函数,不是时间的直接函数,例如
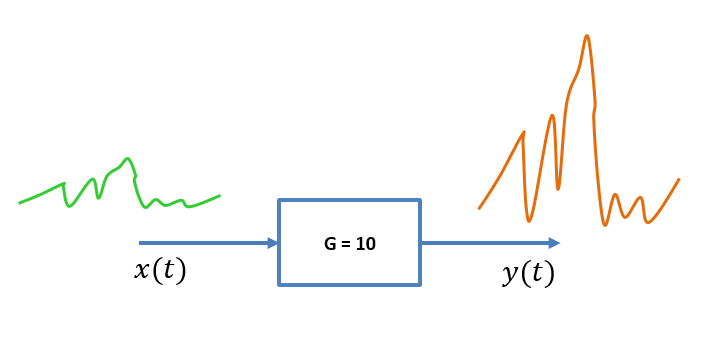
虽然输出随时间变化,但是系统函数不随时间变化
当输入有延迟时,输出也会出现延迟,而且输出形状不发生改变
对线性动态系统建模
状态外推方程的推导
推导状态外推方程:
$$ \boldsymbol{\hat{x}_{n+1,n} =F\hat{x}_{n,n} + G\hat{u}_{n,n} + w_{n} } $$需要对动态系统建模。来计算出动态系统的状态空间表示。以下两个方程是线性时不变(LTI)系统的状态空间表示:
$$ \begin{align} \boldsymbol{\dot{x}(t) = Ax(t) + Bu(t)}\\ \boldsymbol{y(t) = Cx(t) + Du(t)} \end{align} $$$\boldsymbol x$ 状态向量 $\boldsymbol y$ 输出向量 $\boldsymbol A$ 系统动态矩阵 $\boldsymbol B$ 输入矩阵 $\boldsymbol C$ 输出矩阵 $\boldsymbol D$ 馈通矩阵(feedthrough)
为了求出状态转移矩阵$\boldsymbol F$和输入转移矩阵$\boldsymbol G$,需要求解状态空间微分方程
下面图标是求解过程:
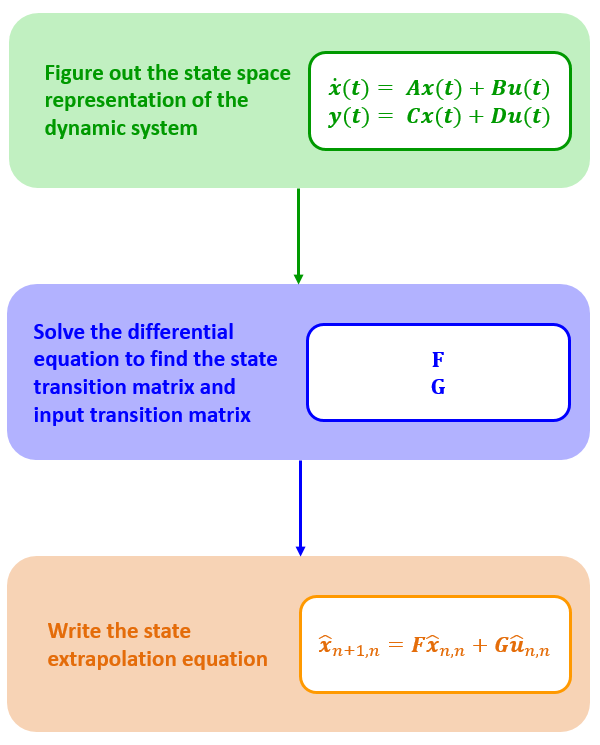
状态空间表示
$$ \begin{align} \boldsymbol{\dot{x}(t) = Ax(t) + Bu(t)}\\ \boldsymbol{y(t) = Cx(t) + Du(t)} \end{align} $$例子:等速运动体
输入为0:
$$ u(t)=0 $$状态空间变量为,位置和速度:
$$ \boldsymbol{x(t)}=\begin{bmatrix} p\\ v \end{bmatrix} $$$$ \boldsymbol{\dot{x}(t) = Ax(t) + Bu(t)} $$$$ \left[ \begin{matrix} \dot{p}\\ \dot{v}\\ \end{matrix} \right] = \boldsymbol{A} \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \boldsymbol{B} \times 0 $$$$ \left[ \begin{matrix} \dot{p}\\ \dot{v}\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] $$动态系统输出:
$$ \boldsymbol{y(t) = Cx(t) + Du(t)} $$$$ p = \boldsymbol{C} \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \boldsymbol{D} \times 0 $$$$ p = \left[ \begin{matrix} 1 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] $$建立高阶动态系统模型
许多动态系统模型是由高阶微分方程描述的。微分方程的阶数是指微分方程中最高导数的数目。阶数为1的微分方程被称为一阶,阶数为2的二阶,等等。
为了解决高阶方程,我们需要通过定义新的变量并将其代入最高阶项,将其还原为一阶微分方程。
降低微分方程阶数的算法
一般的n阶线性微分方程可以表示为n个一阶微分方程的系统。
动态系统的高阶治理方程(governing equation)看起来像:
$$ a_{n}\frac{d^{n}y}{dt^{n} }+ a_{n-1}\frac{d^{n-1}y}{dt^{n-1} }+ \ldots + a_{2}\frac{d^{2}y}{dt^{2} }+a_{1}\frac{d^{1}y}{dt^{1} }+ a_{0}y=u $$治理方程完全表征了系统的动态
减少方程阶数:
- 隔离最高阶导数
- 定义新的变量
- 取状态变量的导数
- 代入最后一个方程
- 写成矩阵形式
可以得到状态空间方程$\boldsymbol {A,B}$的形式:
$$ \boldsymbol{A} = \left[ \begin{matrix} 0 & 1 & 0 & \cdots & 0 & 0\\ 0 & 0 & 1 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 1\\ -\frac{a_{0} }{a_{n} } & -\frac{a_{1} }{a_{n} } & -\frac{a_{2} }{a_{n} } & \cdots & -\frac{a_{n-2} }{a_{n} } & -\frac{a_{n-1} }{a_{n} }\\ \end{matrix} \right] $$$$ \boldsymbol{B} = \left[ \begin{matrix} 0\\ 0\\ \vdots \\ 0\\ \frac{1}{a_{n} }\\ \end{matrix} \right] $$例子-等加速度运动物体
在该例子中有一个额外的力作用于物体
治理方程为牛顿第二定律:
$$ m\ddot{p} = F $$$p$ 为位置位移 $m$ 为质量 $F$ 为额外的力
推导治理方程:
- 隔离高阶导数
- 定义变量
- 取状态变量的导数
- 带入$\ddot{p}$
- 使用向量表示
于是得到方程形式:
$$ \boldsymbol{\dot{x}(t) = Ax(t) + Bu(t)} $$对于动态系统输出:
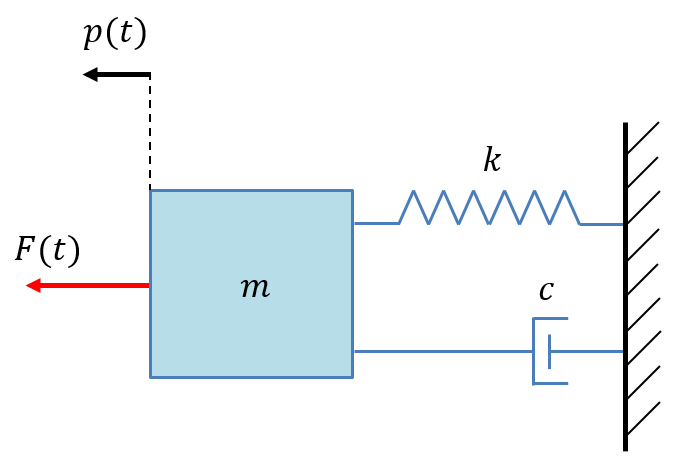
$$ \boldsymbol{y(t) = Cx(t) + Du(t)} $$$$ p = \left[ \begin{matrix} 1 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \left[ \begin{matrix} 0\\ \end{matrix} \right] a $$例子:质量-弹簧-阻尼器系统
基础元素:
- 质量:惯性元素
- 弹簧:弹性元素
- 阻尼:摩擦元素
能量行为:
- 存储能量
- 释放能量
外力$F(t)$,弹簧拉力$kp$,摩擦力$c\dot p$,可以得到
$$ \sum F=F(t)-c\dot{p}-kp=m\ddot p $$步骤:
- 隔离高阶微分项:
- 定义新变量:
- 求导
- 带入
- 写成矩阵
系统输出:
$$ p = \boldsymbol{C} \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \boldsymbol{D} \frac{F}{m} $$$$ p = \left[ \begin{matrix} 1 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \left[ \begin{matrix} 0\\ \end{matrix} \right] \frac{F}{m} $$解微分方程
状态外推方程的形式:
$$ \boldsymbol{\hat{x}_{n+1,n} =F\hat{x}_{n,n} + G\hat{u}_{n,n} } $$我们需要解决描述状态空间的微分方程
无输入变量的动态系统
没有外部输入的LTI动态系统可以用一阶微分方程来描述
$$ \boldsymbol{\dot{x} = Ax} $$$\boldsymbol A$为系统动态矩阵
目标是寻找状态转移矩阵$\boldsymbol F$
$$ \frac{dx}{dt} = kx $$$$ \frac{dx}{x} = kdt $$两边积分:
$$ \int _{x_{0} }^{x_{1} }\frac{1}{x}dx = \int_{0}^{ \Delta t}kdt $$$$ \begin{array}{c} \ln(x_1)-\ln(x_0)=k\Delta t\\ \ln(x_1)=\ln(x_0)+k\Delta t\\ x_1=e^{\ln(x_0)+k\Delta t}\\ x_1=e^{\ln(x_0)}e^{k\Delta t}\\ x_1=x_0e^{k\Delta t} \end{array} $$可以得到
$$ \boldsymbol{\dot{x}=Ax} $$解为:
$$ x_{n+1}= x_{n}e^{\boldsymbol{A} \Delta t} $$状态转移矩阵为:
$$ \boldsymbol{F} = e^{\boldsymbol{A} \Delta t} $$$e^{\boldsymbol{A}t}$为矩阵指数,通过泰勒展开求解:
$$ e^{\boldsymbol{X} }= \sum _{k=0}^{\infty}\frac{1}{k!}\boldsymbol{X}^{k} $$得到:
$$ \boldsymbol{F} = e^{\boldsymbol{A} \Delta t} = \boldsymbol{I} + \boldsymbol{A} \Delta t+ \frac{ \left( \boldsymbol{A} \Delta t \right) ^{2} }{2!}+ \frac{ \left( \boldsymbol{A} \Delta t \right) ^{3} }{3!}+ \frac{ \left( \boldsymbol{A} \Delta t \right) ^{4} }{4!}+ \ldots $$例子:恒定速度运动体
常速模型满足以下微分方程:
$$ \begin{cases} \frac{dp}{dt}=v\\ \frac{dv}{dt}=0\\ \end{cases} $$写成矩阵形式:
$$ \left[ \begin{matrix} \dot{p}\\ \dot{v}\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] $$$$ \boldsymbol{A} = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] $$计算$\boldsymbol{A}^2$
$$ \boldsymbol{A}^{2} = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 0\\ 0 & 0\\ \end{matrix} \right] $$由于$\boldsymbol{A}^2=0$,高阶项都为0
计算状态转移矩阵:
$$ F= e^{\boldsymbol{A} \Delta t} = \boldsymbol{I} + \boldsymbol{A} \Delta t = \left[ \begin{matrix} 1 & 0\\ 0 & 1\\ \end{matrix} \right] + \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \Delta t = \left[ \begin{matrix} 1 & \Delta t\\ 0 & 1\\ \end{matrix} \right] $$$$ x_{n+1} = \boldsymbol{F}x_{n} = \left[ \begin{matrix} 1 & \Delta t\\ 0 & 1\\ \end{matrix} \right] x_{n} $$$$ \left[ \begin{matrix} x_{n+1}\\ \dot{x}_{n+1}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t\\ 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} x_{n}\\ \dot{x}_{n}\\ \end{matrix} \right] $$有输入变量的动态系统
对于零阶保持采样,假设输入是片状常数,状态空间方程的一般解的形式为:
$$ \boldsymbol{\dot{x}(t) = Ax(t) + Bu(t)} $$$$ \boldsymbol{x ( t+ \Delta t )} = {\color{red}{\underbrace{e^{\boldsymbol{A} \Delta t} }_\textrm{F} } } \boldsymbol{x(t)} + {\color{blue}{\underbrace{\int _{0}^{\Delta t} e^{\boldsymbol{A}t}dt\boldsymbol{B} }_\textrm{G} } } \boldsymbol{u(t)} $$去掉$u(t)$则是上面讲的问题
例子:恒定加速度的运动体
恒定加速度运动体的状态空间表示是:
$$ \left[ \begin{matrix} \dot{p}\\ \dot{v}\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \left[ \begin{matrix} 0\\ 1\\ \end{matrix} \right] a $$$$ \boldsymbol{A} = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] $$$$ \boldsymbol{B} = \left[ \begin{matrix} 0\\ 1\\ \end{matrix} \right] $$解方程
$$ \boldsymbol{x ( t+ \Delta t )} = {\color{red}{\underbrace{e^{\boldsymbol{A} \Delta t} }_\textrm{F} } } \boldsymbol{x(t)} + {\color{blue}{\underbrace{\int_{0}^{\Delta t} e^{\boldsymbol{A}t}dt\boldsymbol{B} }_\textrm{G} } } \boldsymbol{u(t)} $$求$\boldsymbol{F}$
$$ \boldsymbol{F} = e^{\boldsymbol{A} \Delta t} $$和已经解的$A = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right]$
$$ \boldsymbol{F} = \left[ \begin{matrix} 1 & \Delta t\\ 0 & 1\\ \end{matrix} \right] $$求$\boldsymbol G$
$$ \boldsymbol{G} = \int_{0}^{ \Delta t}e^{\boldsymbol{A}t}dt \boldsymbol{B} $$由于积分项是指数序列
$$ \int _{0}^{ \Delta t}e^{\boldsymbol{A}t}dt= \Delta t \left( I+ \frac{\boldsymbol{A} \Delta t}{2!}+ \frac{ \left( \boldsymbol{A} \Delta t \right) ^{2} }{3!}+ \frac{ \left( \boldsymbol{A} \Delta t \right) ^{3} }{4!}+ \ldots \right) $$$$ \boldsymbol{A}^{2} = \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 0\\ 0 & 0\\ \end{matrix} \right] $$$$ \int _{0}^{ \Delta t}e^{\boldsymbol{A}t}dt= \Delta t \left( \left[ \begin{matrix} 1 & 0\\ 0 & 1\\ \end{matrix} \right] + \left[ \begin{matrix} 0 & 1\\ 0 & 0\\ \end{matrix} \right] \frac{ \Delta t}{2} \right) = \left[ \begin{matrix} \Delta t & \frac{1}{2}\Delta t^{2}\\ 0 & \Delta t\\ \end{matrix} \right] $$$$ \boldsymbol{G} = \int _{0}^{ \Delta t}e^{\boldsymbol{A}t}dt\boldsymbol{B} = \left[ \begin{matrix} \Delta t & \frac{1}{2}\Delta t^{2}\\ 0 & \Delta t\\ \end{matrix} \right] \left[ \begin{matrix} 0\\ 1\\ \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{2}\Delta t^{2}\\ \Delta t\\ \end{matrix} \right] $$所以,状态外推方程为:
$$ \left[ \begin{matrix} p_{n+1}\\ \dot{p}_{n+1}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t\\ 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} p_{n}\\ \dot{p}_{n}\\ \end{matrix} \right] + \left[ \begin{matrix} \frac{1}{2}\Delta t^{2}\\ \Delta t\\ \end{matrix} \right] a $$例子:质量-弹簧-阻尼器系统
回顾一下,质量-弹簧-阻尼器系统的状态空间表示为:
$$ \left[ \begin{matrix} \dot{p}\\ \dot{v}\\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1\\ -\frac{k}{m} & \frac{c}{m}\\ \end{matrix} \right] \left[ \begin{matrix} p\\ v\\ \end{matrix} \right] + \left[ \begin{matrix} 0\\ \frac{1}{m}\\ \end{matrix} \right] F $$其中
$$ \boldsymbol{A} = \left[ \begin{matrix} 0 & 1\\ -\frac{k}{m} & \frac{c}{m}\\ \end{matrix} \right] $$$$ \boldsymbol{B} = \left[ \begin{matrix} 0\\ \frac{1}{m}\\ \end{matrix} \right] $$在这个例子中,计算矩阵指数并不容易,因为A的高次方并不是零。
这个微分方程的解法已经超出了本教程的范围。你可以使用计算机软件来解决这个方程。如果你想自己解决,你可以在下面几页找到一个有用的指南:
https://www.math24.net/method-matrix-exponential/
http://control.ucsd.edu/mauricio/courses/mae280a/lecture6.pdf
你也可以在下面的演示中找到质量-弹簧-阻尼器系统的二阶微分方程的解(幻灯片29-34):
https://www.engr.sjsu.edu/trhsu/Chapter%204%20Second%20order%20DEs.pdf
协方差外推方程
我们已经在 “一维卡尔曼滤波 “一节中认识了协方差外推公式(或称预测协方差公式)。我假定你已经熟悉了协方差外推(预测)的概念。在本节中,我们将用矩阵符号推导出卡尔曼滤波协方差外推公式:
协方差外推方程的一般形式为:
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$其中 $\boldsymbol{P_{n,n} }$ 为估计不确定性 $\boldsymbol{P_{n+1,n} }$ 为预测不确定性 $\boldsymbol{F}$ 为“线性动态系统建模”一节中得出的状态转换矩阵 $\boldsymbol Q$ 为过程噪声矩阵
无过程噪声的估计不确定性
假设过程噪声为0,则有:
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} } $$协方差:
$$ COV(\boldsymbol{x}) = E \left( \left( \boldsymbol{x - \mu_{x} } \right) \left( \boldsymbol{x - \mu_{x} } \right)^{T} \right) $$因此:
$$ \boldsymbol{P_{n,n} } = E \left( \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right) \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right)^{T} \right) $$根据状态外推方程:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+G\hat{u}_{n,n} } $$得到:
$$ \begin{align} \boldsymbol{P_{n+1,n} } =& E \left( \left( \boldsymbol{\hat{x}_{n+1,n} - \mu_{x_{n+1,n} }} \right) \left( \boldsymbol{\hat{x}_{n+1,n} - \mu_{x_{n+1,n} }} \right)^{T} \right)\\ =& E \left( \left( \boldsymbol{F\hat{x}_{n,n} + G\hat{u}_{n,n} - F\mu_{x_{n,n} } - G\hat{u}_{n,n} } \right) \left( \boldsymbol{F\hat{x}_{n,n} + G\hat{u}_{n,n} - F\mu_{x_{n,n} } - G\hat{u}_{n,n} } \right)^{T} \right)\\ = &E \left( \boldsymbol{F} \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right) \left( \boldsymbol{F} \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right) \right)^{T} \right)\\ &(应用转置矩阵定律)\boldsymbol{(AB)^T=B^TA^T}\\ = &E \left(\boldsymbol{F} \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right) \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right)^{T} \boldsymbol{F^{T} } \right)\\ = & \boldsymbol{F}E \left( \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right) \left( \boldsymbol{\hat{x}_{n,n} - \mu_{x_{n,n} }} \right)^{T} \right) \boldsymbol{F^{T} }\\ =& \boldsymbol{F P_{n,n} F^{T} } \end{align} $$推导过程噪声矩阵Q
动态系统描述为:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+G\hat{u}_{n,n}+w_{n} } $$其中$w_n$为n时刻的测量噪声
在一维卡尔曼滤波中,过程噪声方差用q表示
在多维卡尔曼滤波器中,过程噪声是一个用Q表示的协方差矩阵。
我们已经看到,过程噪声方差对卡尔曼滤波的性能有着至关重要的影响。太小的q会导致滞后误差(见例7)。如果q值过大,卡尔曼滤波将跟随测量结果(见例8)并产生噪声估计
过程噪声在不同状态变量之间可以是独立的。在这种情况下,过程噪声协方差矩阵Q是一个对角矩阵
$$ \boldsymbol{Q} = \left[ \begin{matrix} q_{11} & 0 & \cdots & 0 \\ 0 & q_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & q_{kk} \\ \end{matrix} \right] $$环境过程噪声有两种模式:
- 离散噪声模型
- 连续噪声模型
离散噪声模型
离散噪声类似如下,不同时刻不同,但是区间内是恒定的
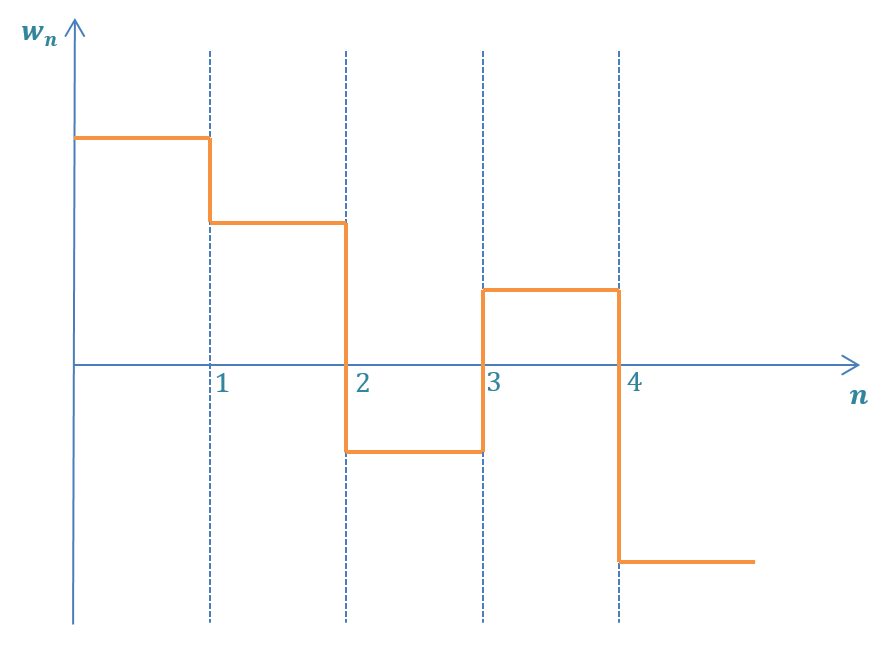
对于常速度模型,过程噪声协方差矩阵为:
$$ \boldsymbol{Q} = \left[ \begin{matrix} V(x) & COV(x,v) \\ COV(v,x) & V(v) \\ \end{matrix} \right] $$我们将用模型的随机加速度方差来表示位置和速度的方差和协方差:$\sigma^2_a$
我将使用期望代数规则推导出矩阵元素
$$ V(v) = \sigma^{2}_{v} = E\left(v^{2}\right) - \mu_{v}^{2} = E \left( \left( a\Delta t\right)^{2}\right) - \left(\mu_{a}\Delta t\right)^{2} = \Delta t^{2}\left( E\left(a^{2}\right) - \mu_{a}^{2} \right) = \Delta t^{2}\sigma^{2}_{a} $$$$ V(x) = \sigma^{2}_{x} = E\left(x^{2}\right) - \mu_{x}^{2} = E \left( \left( \frac{1}{2}a\Delta t^{2}\right)^{2}\right) - \left(\frac{1}{2}\mu_{a}\Delta t^{2}\right)^{2} = \frac{\Delta t^{4} }{4}\left( E\left(a^{2}\right) - \mu_{a}^{2} \right) = \frac{\Delta t^{4} }{4}\sigma^{2}_{a} $$$$ COV(x,v) = COV(v,x) = E\left(xv\right) - \mu_{x}\mu_{v} = E\left( \frac{1}{2}a\Delta t^{2}a\Delta t\right) - \left( \frac{1}{2}\mu_{a}\Delta t^{2}\mu_{a}\Delta t\right) = \frac{\Delta t^{3} }{2}\left( E\left(a^{2}\right) - \mu_{a}^{2} \right) = \frac{\Delta t^{3} }{2}\sigma^{2}_{a} $$所以$\boldsymbol Q$矩阵的结果为:
$$ \boldsymbol{Q} = \sigma^{2}_{a} \left[ \begin{matrix} \frac{\Delta t^{4} }{4} & \frac{\Delta t^{3} }{2} \\ \frac{\Delta t^{3} }{2} & \Delta t^{2} \\ \end{matrix} \right] $$使用状态转换矩阵进行投影
如果动态模型不包括控制输入,我们可以用状态转换矩阵将加速度的随机方差$\sigma^2_a$ 在我们的动态模型上使用状态转换矩阵。让我们定义一个矩阵$Q_a$
$$ \boldsymbol{Q}_{a} = \left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \sigma^{2}_{a} $$过程噪声矩阵问:
$$ \boldsymbol{Q} = \boldsymbol{F}\boldsymbol{Q}_{a}\boldsymbol{F^{T} } $$对于运动模型,$\boldsymbol F$为:
$$ \boldsymbol{F} = \left[ \begin{matrix} 1 & \Delta t & \frac{\Delta t^{2} }{2} \\ 0 & 1 & \Delta t \\ 0 & 0 & 1 \\ \end{matrix} \right] $$$$ \begin{align} \boldsymbol{Q} &= \boldsymbol{F}\boldsymbol{Q}_{a}\boldsymbol{F^{T} }\\ \\ &= \left[ \begin{matrix} 1 & \Delta t & \frac{\Delta t^{2} }{2} \\ 0 & 1 & \Delta t \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 \\ \Delta t & 1 & 0 \\ \frac{\Delta t^{2} }{2} & \Delta t & 1 \\ \end{matrix} \right] \sigma^{2}_{a}\\ \\ &= \left[ \begin{matrix} 0 & 0 & \frac{\Delta t^{2} }{2} \\ 0 & 0 & \Delta t \\ 0 & 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 \\ \Delta t & 1 & 0 \\ \frac{\Delta t^{2} }{2} & \Delta t & 1 \\ \end{matrix} \right] \sigma^{2}_{a}\\ \\ &= \left[ \begin{matrix} \frac{\Delta t^{4} }{4} & \frac{\Delta t^{3} }{2} & \frac{\Delta t^{2} }{2} \\ \frac{\Delta t^{3} }{2} & \Delta t^{2} & \Delta t \\ \frac{\Delta t^{2} }{2} & \Delta t & 1 \\ \end{matrix} \right] \sigma^{2}_{a} \end{align} $$使用控制矩阵进行投影
如果动态模型包括一个控制输入,我们可以更快地计算出$\boldsymbol Q$矩阵。我们可以用状态转换矩阵将加速度的随机方差$\sigma^2_a$投射到我们的动态模型上。
$$ \boldsymbol{Q} = \boldsymbol{G}\sigma^{2}_{a}\boldsymbol{G^{T} } $$$\boldsymbol G$为控制矩阵(或输入转移矩阵)
对于运动模型来说,$\boldsymbol G$矩阵通过以下给定:
$$ \boldsymbol{G} = \left[ \begin{matrix} \frac{\Delta t^{2} }{2} \\ \Delta t \\ \end{matrix} \right] $$$$ \boldsymbol{Q} = \boldsymbol{G}\sigma^{2}_{a}\boldsymbol{G^{T} } = \sigma^{2}_{a}\boldsymbol{G}\boldsymbol{G^{T} } = \sigma^{2}_{a} \left[ \begin{matrix} \frac{\Delta t^{2} }{2} \\ \Delta t \\ \end{matrix} \right] \left[ \begin{matrix} \frac{\Delta t^{2} }{2} & \Delta t \\ \end{matrix} \right] = \sigma^{2}_{a} \left[ \begin{matrix} \frac{\Delta t^{4} }{4} & \frac{\Delta t^{3} }{2} \\ \frac{\Delta t^{3} }{2} & \Delta t^{2} \\ \end{matrix} \right] $$上述任一中方法都能构造离散$\boldsymbol Q$矩阵
连续噪声模型
连续模型假定噪声随时间连续变化
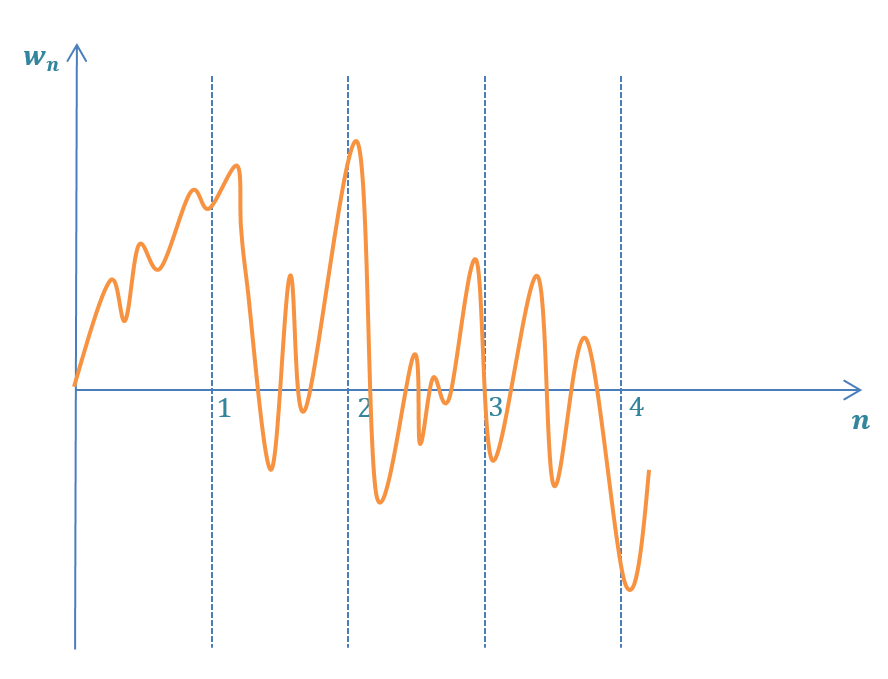
为了得出连续模型$\boldsymbol Q_C$的过程噪声协方差矩阵,我们需要对离散过程噪声协方差矩阵$\boldsymbol Q$进行时间积分。
$$ \boldsymbol{Q_{C} } = \int_{0}^{ \Delta t}\boldsymbol{Q}dt = \int _{0}^{ \Delta t} \sigma^{2}_{a} \left[ \begin{matrix} \frac{t^{4} }{4} & \frac{t^{3} }{2} \\ \frac{t^{3} }{2} & t^{2} \\ \end{matrix} \right] dt = \sigma^{2}_{a} \left[ \begin{matrix} \frac{\Delta t^{5} }{20} & \frac{\Delta t^{4} }{8} \\ \frac{\Delta t^{4} }{8} & \frac{\Delta t^{3} }{3} \\ \end{matrix} \right] $$该怎样选择
在回答这个问题之前,你需要为过程噪声方差选择正确的值。你可以用随机统计公式来计算它,或者根据你的工程实践选择一个合理的值(这是最理想的)。
在雷达领域,$\sigma_a^2$取决于目标特性和模型的完整性。对于机动目标,如飞机,$\sigma_a^2$应相当大。对于非机动目标,如火箭,你可以使用一个较小的$\sigma_a^2$。模型的完整性也是选择过程噪声方差的一个因素。如果你的模型包括像空气阻力这样的环境影响,那么过程噪声的随机性程度就比较小,反之亦然。
一旦你选择了一个合理的过程噪声方差值,你就必须选择噪声模型。它应该是离散的还是连续的?
在这个问题上没有明确的答案。当$\Delta t$非常小时,你可以使用离散噪声模型,当$\Delta t$较大时,最好使用连续噪声模型。我建议尝试这两种模型,并检查哪一种在你的卡尔曼滤波中表现得更好。
测量方程
到目前为止,我们一直在处理未来的问题。我们已经得出了两个卡尔曼滤波预测方程:
- 状态外推方程
- 协方差外推方程
现在讨论测量方程
之前的例子中,我们用$z_n$表示测量值
测量值代表了除了由测量设备引起的随机测量噪声$v_n$之外的真实系统状态。
测量噪声方差$r_n$可以在每次测量中保持不变–例如,如果我们有精度为0.5kg的天平(标准偏差)。另一方面,测量噪声方差$r_n$可以对每次测量不同——例如,如果我们有一个精度为0.5%(标准差)的温度计。在后一种情况下,噪声方差取决于测量的温度。
通常的测量方程矩阵形式如下:
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } $$$\boldsymbol z_n$ 为测量值向量 $\boldsymbol x_n$ 为真实系统状态 $\boldsymbol v_n$ 为随机噪声向量 $\boldsymbol H$ 为观测矩阵
观测矩阵$\boldsymbol H$
在许多情况下,测量值不是理想的系统状态。例如,数字电热计测量的是电流,而系统状态是温度。需要对系统状态(输入)和测量(输出)进行转换。
观察矩阵$\boldsymbol H$的目的是利用线性变换将系统状态转换为输出。以下各章包括观察矩阵的使用实例。
缩放
测距仪向目的地发送信号并接收反射的回波。测量的是发送和接收信号之间的时间延迟。系统状态是范围。
在这种情况下,我们需要进行一个缩放。
$$ \boldsymbol{z_{n} } = \left[ \begin{matrix} \frac{2}{c}\\ \end{matrix} \right] \boldsymbol{x_{n} } + \boldsymbol{v_{n} } $$$$ \boldsymbol{H} = \left[ \begin{matrix} \frac{2}{c}\\ \end{matrix} \right] $$其中: $c$ 为光速 $\boldsymbol x_n$ 为距离 $\boldsymbol z_n$ 为测量得到的延时
状态选择
有时,某些状态是可以测量的,而其他状态则不能测量。例如,一个五维状态矢量的第一、第三和第五个状态是可以测量的,而第二和第四个状态是不可测量的。
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } = \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} {x}_{1}\\ {x}_{2}\\ {x}_{3}\\ {x}_{4}\\ {x}_{5}\\ \end{matrix} \right] + \boldsymbol{v_{n} } = \left[ \begin{matrix} {x}_{1}\\ {x}_{3}\\ {x}_{5}\\ \end{matrix} \right] + \boldsymbol{v_{n} } $$状态合并
有时,一些状态的组合可以被测量,而不是每个单独的状态。例如,也许一个三角形的边长就是这些状态,只有总周长可以被测量。
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } = \left[ \begin{matrix} 1 & 1 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} {x}_{1}\\ {x}_{2}\\ {x}_{3}\\ \end{matrix} \right] + \boldsymbol{v_{n} } = ({x}_{1} + {x}_{2} + {x}_{3}) + \boldsymbol{v_{n} } $$测量方程维度
| 变量 | 描述 | 维度 |
|---|---|---|
| $\boldsymbol x$ | 状态向量 | $n_x \times 1$ |
| $\boldsymbol z$ | 输出向量 | $n_z\times 1$ |
| $\boldsymbol H$ | 观测矩阵 | $n_z\times n_x$ |
| $\boldsymbol v$ | 测量噪声向量 | $n_z \times 1$ |
中期总结
两个预测方程:
- 状态外推方程——根据已知的当前估计,对未来状态进行预测或估计。
- 协方差外推方程——对我们预测的不确定性的衡量。
两个更新方程:
- 状态更新方程——对当前状态的估计,基于已知的过去估计和当前测量。
- 协方差更新方程——对我们估计的不确定性的衡量。
卡尔曼增益方程——更新方程的计算需要。卡尔曼增益实际上是测量和过去估计的一个 “加权 “参数。它定义了过去估计的权重和测量在估计当前状态时的权重。
到目前为止,我们已经学会了矩阵符号中的两个预测方程以及计算主要方程所需的几个辅助方程。
预测方程
状态外推方程
$$ \boldsymbol{\hat{x}_{n+1,n} =F\hat{x}_{n,n} + G\hat{u}_{n,n} + w_{n} } $$其中: $\boldsymbol{\hat{x}_{n+1,n} }$ 为时间为n+1时的系统状态向量预测 $\boldsymbol{\hat{x}_{n,n} }$ 为时间为n的系统状态向量估计 $\boldsymbol{u_{n} }$ 为控制变量或者输入变量 - 影响系统状态的无法测量的输入 $\boldsymbol{w_{n} }$ 为过程噪声或者分布 - 影响系统状态且无法测量 $\boldsymbol F$ 为系统转移矩阵 $\boldsymbol G$ 为控制矩阵或者输入转移矩阵(把控制映射为系统状态变量)
协方差外推矩阵
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$其中: $\boldsymbol{P_{n,n} }$ 为当前状态的估计不确定性(协方差)矩阵 $\boldsymbol{P_{n+1,n} }$ 为下一个状态的预测的估计不确定性(协方差)矩阵 $\boldsymbol{F}$ 为状态转移矩阵 $\boldsymbol Q$ 为过程噪声矩阵
辅助方程
测量方程
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } $$其中: $\boldsymbol{z}_n$ 为测量向量 $\boldsymbol x_n$ 为真实系统状态 $\boldsymbol v_n$ 为随机噪声向量 $\boldsymbol H$ 为观测矩阵
协方差方程
术语$w$和$v$对应于过程和测量噪声向量,有趣的是它们通常不直接出现在感兴趣的方程中,因为它们是未知的。对应于过程和测量噪声向量,有趣的是,它们通常不直接出现在感兴趣的方程中,因为它们是未知的。
相反,这些术语被用来模拟方程本身的不确定性(或噪声)。
所有协方差方程都是协方差矩阵的形式:
$$ E(ee^T) $$测量不确定性
$$ \boldsymbol{R_{n} } = E\left( \boldsymbol{v_{n}v_{n}^{T} } \right) $$其中: $\boldsymbol R_n$ 为测量值的协方差矩阵 $\boldsymbol v_n$ 为测量误差
过程噪声不确定性
$$ \boldsymbol{Q_{n} } = E\left( \boldsymbol{w_{n}w_{n}^{T} } \right) $$其中: $\boldsymbol Q_n$ 为过程噪声的协方差矩阵 $\boldsymbol w_n$ 为过程噪声
估计不确定性
$$ \boldsymbol{P_{n,n} } = E\left( \boldsymbol{e_{n}e_{n}^{T} } \right) = E\left( \left( \boldsymbol{x_{n} - \hat{x}_{n,n} } \right) \left( \boldsymbol{x_{n} - \hat{x}_{n,n} } \right)^{T} \right) $$其中: $\boldsymbol{P_{n,n} }$ 为估计误差的协方差矩阵 $\boldsymbol e_n$ 为估计误差 $\boldsymbol x_n$ 为真实系统状态(隐藏状态) $\boldsymbol{\hat x_{n,n} }$ 为时间为n的时候的估计系统状态向量
状态更新方程
更多的内容请回去看[$\alpha-\beta-\gamma$滤波](# $\alpha-\beta-\gamma$滤波) 和 [一维卡尔曼滤波](# 一维卡尔曼滤波)
状态更新方程的形式为:
$$ \boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )} $$其中: $\boldsymbol{\hat{x}_{n,n} }$ 为时间为n时的估计系统状态向量 $\boldsymbol{\hat{x}_{n,n-1} }$ 为时间为n-1时的预测系统状态向量 $\boldsymbol H_n$ 为卡尔曼增益 $\boldsymbol z_n$为测量值 $\boldsymbol H$ 为观测矩阵
你应该熟悉状态更新方程的所有组成部分,除了以矩阵形式表示的卡尔曼增益。我们稍后将推导出卡尔曼增益。
你应该注意尺寸。例如,如果状态向量有5个维度,而只有3个维度是可测量的(第一、第三和第五状态)。
$$ \boldsymbol{x(n)} = \left[ \begin{matrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ x_{5}\\ \end{matrix} \right] \boldsymbol{z(n)} = \left[ \begin{matrix} z_{1}\\ z_{3}\\ z_{5}\\ \end{matrix} \right] $$观测矩阵应该是$3\times5$的矩阵:
$$ \boldsymbol{H} = \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] $$展开$\left( \boldsymbol{ z_{n} - H \hat{x}_{n,n-1} } \right)$得到:
$$ \left( \boldsymbol{ z_{n} - H \hat{x}_{n,n-1} } \right) = \left[ \begin{matrix} z_{1}\\ z_{3}\\ z_{5}\\ \end{matrix} \right] - \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{1}\\ \hat{x}_{2}\\ \hat{x}_{3}\\ \hat{x}_{4}\\ \hat{x}_{5}\\ \end{matrix} \right] = \left[ \begin{matrix} (z_{1} - \hat{x}_{1})\\ (z_{3} - \hat{x}_{3})\\ (z_{5} - \hat{x}_{5})\\ \end{matrix} \right] $$卡尔曼增益为敌应该是$5\times3$
状态更新方程维度
| 变量 | 描述 | 维度 |
|---|---|---|
| $\boldsymbol x$ | 状态向量 | $n_x \times 1$ |
| $\boldsymbol z$ | 输出向量 | $n_z\times 1$ |
| $\boldsymbol H$ | 观测矩阵 | $n_z\times n_x$ |
| $\boldsymbol K$ | 测量噪声向量 | $n_x \times n_z$ |
协方差更新方程
$$ \boldsymbol{ P_{n,n} = \left( I - K_{n}H \right) P_{n,n-1} \left( I - K_{n}H \right)^{T} + K_{n}R_{n}K_{n}^{T} } $$其中: $\boldsymbol{P_{n,n} }$ 估计不确定性(协方差)矩阵当前状态 $\boldsymbol{P_{n,n-1} }$ 之前估计不确定性(协方差)矩阵对于当前状态的预测 $\boldsymbol K_n$ 卡尔曼增益 $\boldsymbol H$ 观测矩阵 $\boldsymbol R_n$ 测量不确定性(测量噪声协方差矩阵)
协方差更新方程推导
对于推导,我将使用以下四个方程式:
| 方程序号 | 方程 | 笔记 |
|---|---|---|
| 1 | $\boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )}$ | 状态更新方程 |
| 2 | $\boldsymbol{z_{n} = Hx_{n} + v_{n} }$ | 测量方程 |
| 3 | $\boldsymbol{P_{n,n} } = E\left( \boldsymbol{e_{n}e_{n}^{T} } \right) = E\left( \left( \boldsymbol{x_{n} - \hat{x}_{n,n} } \right) \left( \boldsymbol{x_{n} - \hat{x}_{n,n} } \right)^{T} \right)$ | 估计不确定性 |
| 4 | $\boldsymbol{R_{n} } = E\left( \boldsymbol{v_{n}v_{n}^{T} } \right)$ | 测量不确定性 |
推导过程见 https://www.kalmanfilter.net/covUpdate.html
卡尔曼增益方程推导
一般形式:
$$ \boldsymbol{ K_{n} = P_{n,n-1}H^{T}\left( HP_{n,n-1}H^{T} + R_{n} \right)^{-1} } $$其中: $\boldsymbol{K_n}$ 为卡尔曼增益 $\boldsymbol{P_{n,n-1} }$ 为之前的估计不确定性(协方差)矩阵对当前状态的预测 $\boldsymbol{H}$ 为观测矩阵 $\boldsymbol{R_n}$ 为测量不确定性(测量噪声协方差矩阵)
https://www.kalmanfilter.net/kalmanGain.html
简化的协方差更新方程
https://www.kalmanfilter.net/simpCovUpdate.html
总结
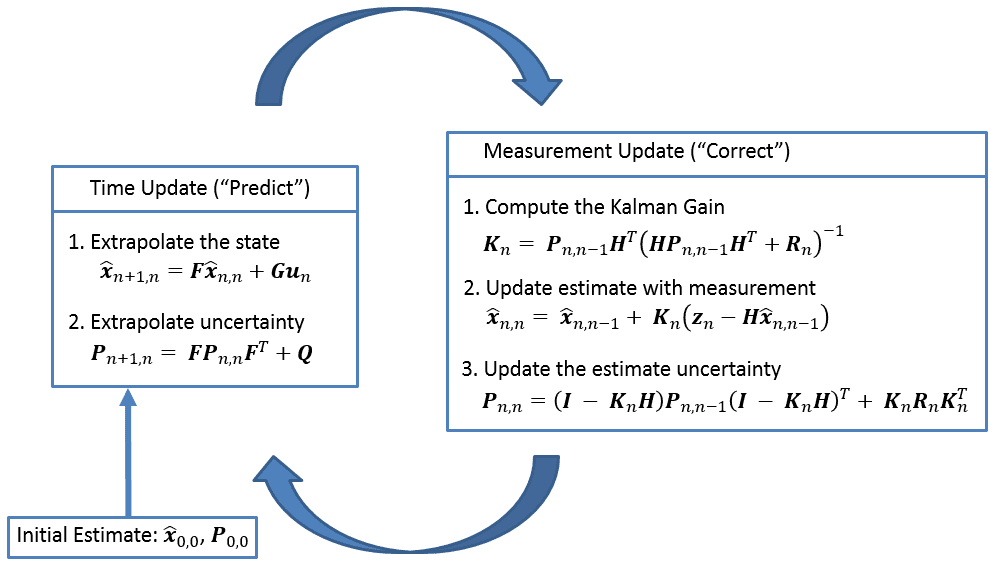
卡尔曼滤波操作处于“预测-纠正”循环,如图
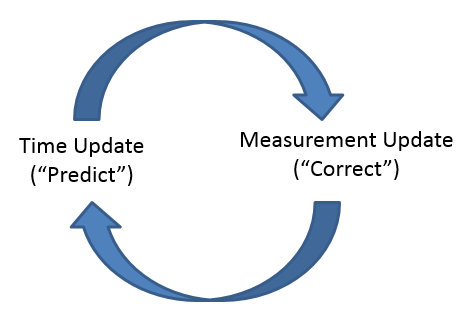
一旦初始化,卡尔曼滤波器将预测下一个时间步骤的系统状态。它还提供预测的不确定性。
一旦收到测量结果,卡尔曼滤波器会更新(或修正)预测和当前状态的不确定性。同样,卡尔曼滤波器也会预测下一个状态,以此类推。
下图提供了卡尔曼滤波器操作的完整画面。
| 方程 | 方程名称 | 其他名称 | |
|---|---|---|---|
| 预测 | $\boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_{n}}$ | 状态外推 | 预测方程 转移方程 动态模型 状态空间方程 |
| $\boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q}$ | 协方差外推 | 预测协方差方程 | |
| 更新(校正) | $\boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )}$ | 状态更新 | 滤波方程 |
| $\boldsymbol{ P_{n,n} = \left( I - K_{n}H \right) P_{n,n-1} \left( I - K_{n}H \right)^{T} + K_{n}R_{n}K_{n}^{T} }$ | 协方差更新 | 校正方程 | |
| $\boldsymbol{ K_{n} = P_{n,n-1}H^{T}\left( HP_{n,n-1}H^{T} + R_{n} \right)^{-1} }$ | 卡尔曼增益 | 权重方程 | |
| 辅助方程 | $\boldsymbol{z_{n} = Hx_{n}}$ | 测量方程 | |
| $\boldsymbol{R_{n}} = E\left( \boldsymbol{v_{n}v_{n}^{T}} \right)$ | 测量不确定性 | 测量误差 | |
| $\boldsymbol{Q_{n}} = E\left( \boldsymbol{w_{n}w_{n}^{T}} \right)$ | 过程噪声不确定性 | 过程噪声误差 | |
| $\boldsymbol{P_{n,n}} = E\left( \boldsymbol{e_{n}e_{n}^{T}} \right) = E\left( \left( \boldsymbol{x_{n} - \hat{x}_{n,n}} \right) \left( \boldsymbol{x_{n} - \hat{x}_{n,n}} \right)^{T} \right)$ | 估计不确定性 | 估计错误 |
维度
| 术语 | 名称 | 其他术语 | 维度 |
|---|---|---|---|
| $\boldsymbol{x}$ | 状态向量 | $n_{x} \times$ | |
| $\boldsymbol{z}$ | 输出向量 | $\boldsymbol{y}$ | $n_{z} \times 1$ |
| $\boldsymbol{F}$ | 状态转移矩阵 | $\boldsymbol{\Phi,A}$ | $n_{x} \times n_{x}$ |
| $\boldsymbol{u}$ | 输入变量 | $n_{u} \times 1$ | |
| $\boldsymbol{G}$ | 控制矩阵 | $\boldsymbol{B}$ | $n_{x} \times n_{u}$ |
| $\boldsymbol{P}$ | 估计不确定性 | $\boldsymbol{\Sigma}$ | $n_{x} \times n_{x}$ |
| $\boldsymbol{Q}$ | 过程噪声不确定性 | $n_{x} \times n_{x}$ | |
| $\boldsymbol{R}$ | 测量不确定性 | $n_{z} \times n_{z}$ | |
| $\boldsymbol{w}$ | 过程噪声向量 | $\boldsymbol{y}$ | $n_{x} \times 1$ |
| $\boldsymbol{v}$ | 测量噪声向量 | $n_{z} \times 1$ | |
| $\boldsymbol{H}$ | 观测矩阵 | $\boldsymbol{C}$ | $n_{z} \times n_{x}$ |
| $\boldsymbol{K}$ | 卡尔曼增益 | $n_{x} \times n_{z}$ | |
| $\boldsymbol{n}$ | 离散时间索引 | $\boldsymbol{k}$ |
例子
例子9-汽车位置估计
估计在$XY$平面运动的车辆
车上有定位传感器能够给出$X$和$Y$的坐标
状态外推方程
一般形式:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_n+w_n} $$其中: $\boldsymbol{\hat{x}_{n+1,n} }$ 为时间为$n+1$时预测系统状态向量 $\boldsymbol{\hat{x}_{n,n} }$ 为时间为$n$时系统状态向量 $\boldsymbol{u_n}$ 为控制变量或者输入变量-对系统的可测量的(确定性的)输入 $\boldsymbol{w_n}$ 为过程噪声或干扰–影响状态的不可测量的输入 $\boldsymbol{F}$ 为系统转移矩阵 $\boldsymbol{G}$ 为控制矩阵或输入转换矩阵(将控制变量映射到状态变量)
在该例子中,没有输入变量$\boldsymbol u$,我们不需要控制输入,所以状态外推方程可以简化为:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}} $$系统状态$\boldsymbol x_n$定义为:
$$ \boldsymbol{x_{n}}= \left[ \begin{matrix} \hat{x}_{n}\\ \hat{\dot{x}}_{n}\\ \hat{\ddot{x}}_{n}\\ \hat{y}_{n}\\ \hat{\dot{y}}_{n}\\ \hat{\ddot{y}}_{n}\\ \end{matrix} \right] $$时间为n+1时外推车辆状态可以描述为:
$$ \begin{cases} \hat{x}_{n+1,n} = \hat{x}_{n,n} + \hat{\dot{x}}_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{x}}_{n,n}\Delta t^{2}\\ \hat{\dot{x}}_{n+1,n} = \hat{\dot{x}}_{n,n} + \hat{\ddot{x}}_{n,n}\Delta t\\ \hat{\ddot{x}}_{n+1,n} = \hat{\ddot{x}}_{n,n}\\ \hat{y}_{n+1,n} = \hat{y}_{n,n} + \hat{\dot{y}}_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{y}}_{n,n}\Delta t^{2}\\ \hat{\dot{y}}_{n+1,n} = \hat{\dot{y}}_{n,n} + \hat{\ddot{y}}_{n,n}\Delta t\\ \hat{\ddot{y}}_{n+1,n} = \hat{\ddot{y}}_{n,n}\\ \hat{z}_{n+1,n} = \hat{z}_{n,n} + \hat{\dot{z}}_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{z}}_{n,n}\Delta t^{2}\\ \hat{\dot{z}}_{n+1,n} = \hat{\dot{z}}_{n,n} + \hat{\ddot{z}}_{n,n}\Delta t\\ \hat{\ddot{z}}_{n+1,n} = \hat{\ddot{z}}_{n,n} \end{cases} $$写成矩阵形式为:
$$ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{\dot{x}}_{n+1,n}\\ \hat{\ddot{x}}_{n+1,n}\\ \hat{y}_{n+1,n}\\ \hat{\dot{y}}_{n+1,n}\\ \hat{\ddot{y}}_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t & 0.5\Delta t^{2} & 0 & 0 & 0\\ 0 & 1 & \Delta t & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & \Delta t & 0.5\Delta t^{2}\\ 0 & 0 & 0 & 0 & 1 & \Delta t\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{\dot{x}}_{n,n}\\ \hat{\ddot{x}}_{n,n}\\ \hat{y}_{n,n}\\ \hat{\dot{y}}_{n,n}\\ \hat{\ddot{y}}_{n,n}\\ \end{matrix} \right] $$协方差外推方程
一般形式:
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$其中 $\boldsymbol{P_{n,n} }$ 为估计不确定性 $\boldsymbol{P_{n+1,n} }$ 为预测不确定性 $\boldsymbol{F}$ 为“线性动态系统建模”一节中得出的状态转换矩阵 $\boldsymbol Q$ 为过程噪声矩阵
估计不确定性的矩阵形式为:
$$ \boldsymbol{P} = \left[ \begin{matrix} p_{x} & p_{x\dot{x}} & p_{x\ddot{x}} & p_{xy} & p_{x\dot{y}} & p_{x\ddot{y}} \\ p_{\dot{x}x} & p_{\dot{x}} & p_{\dot{x}\ddot{x}} & p_{\dot{x}y} & p_{\dot{x}\dot{y}} & p_{\dot{x}\ddot{y}} \\ p_{\ddot{x}x} & p_{\ddot{x}\dot{x}} & p_{\ddot{x}} & p_{\ddot{x}y} & p_{\ddot{x}\dot{y}} & p_{\ddot{x}\ddot{y}} \\ p_{yx} & p_{y\dot{x}} & p_{y\ddot{x}} & p_{y} & p_{y\dot{y}} & p_{y\ddot{y}} \\ p_{\dot{y}x} & p_{\dot{y}\dot{x}} & p_{\dot{y}\ddot{x}} & p_{\dot{y}y} & p_{\dot{y}} & p_{\dot{y}\ddot{y}} \\ p_{\ddot{y}x} & p_{\ddot{y}\dot{x}} & p_{\ddot{y}\ddot{x}} & p_{\ddot{y}y} & p_{\ddot{y}\dot{y}} & p_{\ddot{y}} \\ \end{matrix} \right] $$其中:
- $p_x$为$\boldsymbol{X}$坐标位置估计的方差
- $p_{\dot{x}}$为$\boldsymbol{X}$坐标速度估计的方差
- $p_{\ddot{x}}$为$\boldsymbol{X}$坐标加速度估计的方差
- $p_y$为$\boldsymbol{Y}$坐标位置估计的方差
- $p_{\dot{y}}$为$\boldsymbol{Y}$坐标速度估计的方差
- $p_{\ddot{y}}$为$\boldsymbol{Y}$坐标加速度估计的方差
- 非对角线的为协方差
假设估计误差在$\boldsymbol{X}$和$\boldsymbol{Y}$轴不相关,矩阵变为:
$$ \boldsymbol{P} = \left[ \begin{matrix} p_{x} & p_{x\dot{x}} & p_{x\ddot{x}} & 0 & 0 & 0 \\ p_{\dot{x}x} & p_{\dot{x}} & p_{\dot{x}\ddot{x}} & 0 & 0 & 0 \\ p_{\ddot{x}x} & p_{\ddot{x}\dot{x}} & p_{\ddot{x}} & 0 & 0 & 0 \\ 0 & 0 & 0 & p_{y} & p_{y\dot{y}} & p_{y\ddot{y}} \\ 0 & 0 & 0 & p_{\dot{y}y} & p_{\dot{y}} & p_{\dot{y}\ddot{y}} \\ 0 & 0 & 0 & p_{\ddot{y}y} & p_{\ddot{y}\dot{y}} & p_{\ddot{y}} \\ \end{matrix} \right] $$已经推导出状态转移矩阵$\boldsymbol{F}$。现在需要推导过程噪声矩阵$\boldsymbol{Q}$
过程噪声矩阵
二维过程噪声常加速度模型如下:
$$ \boldsymbol{Q} = \left[ \begin{matrix} \sigma_{x}^{2} & \sigma_{x\dot{x}}^{2} & \sigma_{x\ddot{x}}^{2} & \sigma_{xy}^{2} & \sigma_{x\dot{y}}^{2} & \sigma_{x\ddot{y}}^{2} \\ \sigma_{\dot{x}x}^{2} & \sigma_{\dot{x}}^{2} & \sigma_{\dot{x}\ddot{x}}^{2} & \sigma_{\dot{x}y}^{2} & \sigma_{\dot{x}\dot{y}}^{2} & \sigma_{\dot{x}\ddot{y}}^{2} \\ \sigma_{\ddot{x}x}^{2} & \sigma_{\ddot{x}\dot{x}}^{2} & \sigma_{\ddot{x}}^{2} & \sigma_{\ddot{x}y}^{2} & \sigma_{\ddot{x}\dot{y}}^{2} & \sigma_{\ddot{x}\ddot{y}}^{2} \\ \sigma_{yx}^{2} & \sigma_{y\dot{x}}^{2} & \sigma_{y\ddot{x}}^{2} & \sigma_{y}^{2} & \sigma_{y\dot{y}}^{2} & \sigma_{y\ddot{y}}^{2} \\ \sigma_{\dot{y}x}^{2} & \sigma_{\dot{y}\dot{x}}^{2} & \sigma_{\dot{y}\ddot{x}}^{2} & \sigma_{\dot{y}y}^{2} & \sigma_{\dot{y}}^{2} & \sigma_{\dot{y}\ddot{y}}^{2} \\ \sigma_{\ddot{y}x}^{2} & \sigma_{\ddot{y}\dot{x}}^{2} & \sigma_{\ddot{y}\ddot{x}}^{2} & \sigma_{\ddot{y}y}^{2} & \sigma_{\ddot{y}\dot{y}}^{2} & \sigma_{\ddot{y}}^{2} \\ \end{matrix} \right] $$假设过程噪声在$\boldsymbol{X}$和$\boldsymbol{Y}$轴不相关,变为:
$$ \boldsymbol{Q} = \left[ \begin{matrix} \sigma_{x}^{2} & \sigma_{x\dot{x}}^{2} & \sigma_{x\ddot{x}}^{2} & 0 & 0 & 0 \\ \sigma_{\dot{x}x}^{2} & \sigma_{\dot{x}}^{2} & \sigma_{\dot{x}\ddot{x}}^{2} & 0 & 0 & 0 \\ \sigma_{\ddot{x}x}^{2} & \sigma_{\ddot{x}\dot{x}}^{2} & \sigma_{\ddot{x}}^{2} & 0 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{y}^{2} & \sigma_{y\dot{y}}^{2} & \sigma_{y\ddot{y}}^{2} \\ 0 & 0 & 0 & \sigma_{\dot{y}y}^{2} & \sigma_{\dot{y}}^{2} & \sigma_{\dot{y}\ddot{y}}^{2} \\ 0 & 0 & 0 & \sigma_{\ddot{y}y}^{2} & \sigma_{\ddot{y}\dot{y}}^{2} & \sigma_{\ddot{y}}^{2} \\ \end{matrix} \right] $$根据常加速度模型推导出来的$\boldsymbol{Q}$为:
$$ \boldsymbol{Q} = \left[ \begin{matrix} \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} & \frac{\Delta t^{2}}{2} & 0 & 0 & 0 \\ \frac{\Delta t^{3}}{2} & \Delta t^{2} & \Delta t & 0 & 0 & 0 \\ \frac{\Delta t^{2}}{2} & \Delta t & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} & \frac{\Delta t^{2}}{2} \\ 0 & 0 & 0 & \frac{\Delta t^{3}}{2} & \Delta t^{2} & \Delta t \\ 0 & 0 & 0 & \frac{\Delta t^{2}}{2} & \Delta t & 1 \\ \end{matrix} \right] \sigma_{a}^{2} $$其中:
- $\Delta t$为测量间隔时间
- $\sigma_a^2$为加速度的随机方差
所以该例子的协方差状态外推方差为:
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$$$ \left[ \begin{matrix} p_{x_{n+1,n}} & p_{x\dot{x}_{n+1,n}} & p_{x\ddot{x}_{n+1,n}} & 0 & 0 & 0 \\ p_{\dot{x}x_{n+1,n}} & p_{\dot{x}_{n+1,n}} & p_{\dot{x}\ddot{x}_{n+1,n}} & 0 & 0 & 0 \\ p_{\ddot{x}x_{n+1,n}} & p_{\ddot{x}\dot{x}_{n+1,n}} & p_{\ddot{x}_{n+1,n}} & 0 & 0 & 0 \\ 0 & 0 & 0 & p_{y_{n+1,n}} & p_{y\dot{y}_{n+1,n}} & p_{y\ddot{y}_{n+1,n}} \\ 0 & 0 & 0 & p_{\dot{y}y_{n+1,n}} & p_{\dot{y}_{n+1,n}} & p_{\dot{y}\ddot{y}_{n+1,n}} \\ 0 & 0 & 0 & p_{\ddot{y}y_{n+1,n}} & p_{\ddot{y}\dot{y}_{n+1,n}} & p_{\ddot{y}_{n+1,n}} \\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t & 0.5\Delta t^{2} & 0 & 0 & 0\\ 0 & 1 & \Delta t & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & \Delta t & 0.5\Delta t^{2}\\ 0 & 0 & 0 & 0 & 1 & \Delta t\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \times \left[ \begin{matrix} p_{x_{n,n}} & p_{x\dot{x}_{n,n}} & p_{x\ddot{x}_{n,n}} & 0 & 0 & 0 \\ p_{\dot{x}x_{n,n}} & p_{\dot{x}_{n,n}} & p_{\dot{x}\ddot{x}_{n,n}} & 0 & 0 & 0 \\ p_{\ddot{x}x_{n,n}} & p_{\ddot{x}\dot{x}_{n,n}} & p_{\ddot{x}_{n,n}} & 0 & 0 & 0 \\ 0 & 0 & 0 & p_{y_{n,n}} & p_{y\dot{y}_{n,n}} & p_{y\ddot{y}_{n,n}} \\ 0 & 0 & 0 & p_{\dot{y}y_{n,n}} & p_{\dot{y}_{n,n}} & p_{\dot{y}\ddot{y}_{n,n}} \\ 0 & 0 & 0 & p_{\ddot{y}y_{n,n}} & p_{\ddot{y}\dot{y}_{n,n}} & p_{\ddot{y}_{n,n}} \\ \end{matrix} \right] \times \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 & 0\\ \Delta t & 1 & 0 & 0 & 0 & 0\\ 0.5\Delta t^{2} & \Delta t & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & \Delta t & 1 & 0\\ 0 & 0 & 0 & 0.5\Delta t^{2} & \Delta t & 1\\ \end{matrix} \right] + \left[ \begin{matrix} \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} & \frac{\Delta t^{2}}{2} & 0 & 0 & 0 \\ \frac{\Delta t^{3}}{2} & \Delta t^{2} & \Delta t & 0 & 0 & 0 \\ \frac{\Delta t^{2}}{2} & \Delta t & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} & \frac{\Delta t^{2}}{2} \\ 0 & 0 & 0 & \frac{\Delta t^{3}}{2} & \Delta t^{2} & \Delta t \\ 0 & 0 & 0 & \frac{\Delta t^{2}}{2} & \Delta t & 1 \\ \end{matrix} \right] \sigma_{a}^{2} $$测量方程
一般形式如下:
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } $$$\boldsymbol z_n$ 为测量值向量 $\boldsymbol x_n$ 为真实系统状态 $\boldsymbol v_n$ 为随机噪声向量 $\boldsymbol H$ 为观测矩阵
由于测量值仅为$\boldsymbol{X}$和$\boldsymbol{Y}$轴车辆坐标位置,所以:$\boldsymbol{z_{n}} = \left[ \begin{matrix} x_{n,measured}\\ y_{n,measured}\\ \end{matrix}\right]$
$$ \boldsymbol{z_{n} = Hx_{n}} $$$$ \left[ \begin{matrix} x_{n,measured}\\ y_{n,measured}\\ \end{matrix}\right] = \boldsymbol{H} \left[ \begin{matrix} x_{n}\\ \dot{x}_{n} \\ \ddot{x}_{n}\\ y_{n} \\ \dot{y}_{n} \\ \ddot{y}_{n}\\ \end{matrix} \right] $$根据维度信息和以上条件,可以求出测量矩阵:
$$ \boldsymbol{H} = \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{matrix} \right] $$测量不确定性
测量协方差矩阵为:
$$ \boldsymbol{R_{n}} = \left[ \begin{matrix} \sigma_{x_{m}}^{2} & \sigma_{yx_{m}}^{2} \\ \sigma_{xy_{m}}^{2} & \sigma_{y_{m}}^{2} \\ \end{matrix} \right] $$下标$m$代表测量不确定性
假设$x$和$y$的测量不相关,误差也不相关:
$$ \boldsymbol{R_{n}} = \left[ \begin{matrix} \sigma_{x_{m}}^{2} & 0 \\ 0 & \sigma_{y_{m}}^{2} \\ \end{matrix} \right] $$在现实应用中,测量不确定性和测量可能不同。很多系统的测量不确定性取决于SNR(信噪比)、传感器和目标的夹角、信号频率和其他参数等。
例子中做了简化,假设测量不确定性是个常量:
$$ \boldsymbol{R_{1}} = \boldsymbol{R_{2}} ... \boldsymbol{R_{n-1}} = \boldsymbol{R_{n}} = \boldsymbol{R} $$卡尔曼增益
一般形式:
$$ \boldsymbol{ K_{n} = P_{n,n-1}H^{T}\left( HP_{n,n-1}H^{T} + R_{n} \right)^{-1} } $$其中: $\boldsymbol{K_n}$ 为卡尔曼增益 $\boldsymbol{P_{n,n-1} }$ 为之前的估计不确定性(协方差)矩阵对当前状态的预测 $\boldsymbol{H}$ 为观测矩阵 $\boldsymbol{R_n}$ 为测量不确定性(测量噪声协方差矩阵)
根据已经推导的卡尔曼增益:
$$ \left[ \begin{matrix} K_{1,1_{n}} & K_{1,2_{n}} \\ K_{2,1_{n}} & K_{2,2_{n}} \\ K_{3,1_{n}} & K_{3,2_{n}} \\ K_{4,1_{n}} & K_{4,2_{n}} \\ K_{5,1_{n}} & K_{5,2_{n}} \\ K_{6,1_{n}} & K_{6,2_{n}} \\ \end{matrix} \right] = \left[ \begin{matrix} p_{x_{n,n-1}} & p_{x\dot{x}_{n,n-1}} & p_{x\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ p_{\dot{x}x_{n,n-1}} & p_{\dot{x}_{n,n-1}} & p_{\dot{x}\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ p_{\ddot{x}x_{n,n-1}} & p_{\ddot{x}\dot{x}_{n,n-1}} & p_{\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ 0 & 0 & 0 & p_{y_{n,n-1}} & p_{y\dot{y}_{n,n-1}} & p_{y\ddot{y}_{n,n-1}} \\ 0 & 0 & 0 & p_{\dot{y}y_{n,n-1}} & p_{\dot{y}_{n,n-1}} & p_{\dot{y}\ddot{y}_{n,n-1}} \\ 0 & 0 & 0 & p_{\ddot{y}y_{n,n-1}} & p_{\ddot{y}\dot{y}_{n,n-1}} & p_{\ddot{y}_{n,n-1}} \\ \end{matrix} \right] \left[ \begin{matrix} 1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right] \times \left( \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{matrix}\right] \left[ \begin{matrix} p_{x_{n,n-1}} & p_{x\dot{x}_{n,n-1}} & p_{x\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ p_{\dot{x}x_{n,n-1}} & p_{\dot{x}_{n,n-1}} & p_{\dot{x}\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ p_{\ddot{x}x_{n,n-1}} & p_{\ddot{x}\dot{x}_{n,n-1}} & p_{\ddot{x}_{n,n-1}} & 0 & 0 & 0 \\ 0 & 0 & 0 & p_{y_{n,n-1}} & p_{y\dot{y}_{n,n-1}} & p_{y\ddot{y}_{n,n-1}} \\ 0 & 0 & 0 & p_{\dot{y}y_{n,n-1}} & p_{\dot{y}_{n,n-1}} & p_{\dot{y}\ddot{y}_{n,n-1}} \\ 0 & 0 & 0 & p_{\ddot{y}y_{n,n-1}} & p_{\ddot{y}\dot{y}_{n,n-1}} & p_{\ddot{y}_{n,n-1}} \\ \end{matrix} \right] \left[ \begin{matrix} 1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ \end{matrix} \right] + \left[ \begin{matrix} \sigma_{x_{m}}^{2} & 0 \\ 0 & \sigma_{y_{m}}^{2} \\ \end{matrix} \right] \right)^{-1} $$状态更新方程
状态更新方程的形式为:
$$ \boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )} $$其中: $\boldsymbol{\hat{x}_{n,n} }$ 为时间为n时的估计系统状态向量 $\boldsymbol{\hat{x}_{n,n-1} }$ 为时间为n-1时的预测系统状态向量 $\boldsymbol {H_n}$ 为卡尔曼增益 $\boldsymbol {z_n}$为测量值 $\boldsymbol {H}$ 为观测矩阵
协方差更新方程
$$ \boldsymbol{ P_{n,n} = \left( I - K_{n}H \right) P_{n,n-1} \left( I - K_{n}H \right)^{T} + K_{n}R_{n}K_{n}^{T} } $$其中: $\boldsymbol{P_{n,n} }$ 估计不确定性(协方差)矩阵当前状态 $\boldsymbol{P_{n,n-1} }$ 之前估计不确定性(协方差)矩阵对于当前状态的预测 $\boldsymbol K_n$ 卡尔曼增益 $\boldsymbol H$ 观测矩阵 $\boldsymbol R_n$ 测量不确定性(测量噪声协方差矩阵)
数值例子
解数值例子。假设车辆在$\boldsymbol{X}$方向上常速移动。在行走400m后车辆右转转弯半径为300m,在转弯过程中,车辆经历加速过程,如下图所示
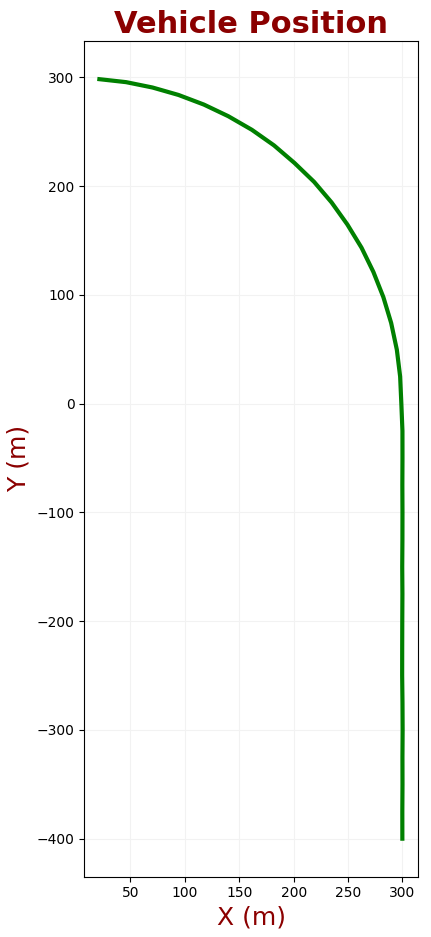
- 测量间隔:$\operatorname{\Delta}t=1s$
- 随机加速度标准差:$\sigma^2_a=0.15m/s^2$
- 测量误差标准差为:$\sigma_{x_m}=\sigma_{x_m}=3m$
- 状态转移矩阵$\boldsymbol{F}$为:
- 过程噪声矩阵$\boldsymbol{Q}$为:
- 测量不确定性$\boldsymbol{R}$
- 测量数据为:
x = [-393.66, -375.93, -351.04, -328.96, -299.35, -273.36, -245.89, -222.58, -198.03, -174.17, -146.32, -123.72, -103.47, -78.23, -52.63, -23.34, 25.96, 49.72, 76.94, 95.38, 119.83, 144.01, 161.84, 180.56, 201.42, 222.62, 239.4, 252.51, 266.26, 271.75, 277.4, 294.12, 301.23, 291.8, 299.89]
y = [300.4, 301.78, 295.1, 305.19, 301.06, 302.05, 300, 303.57, 296.33, 297.65, 297.41, 299.61, 299.6, 302.39, 295.04, 300.09, 294.72, 298.61, 294.64, 284.88, 272.82, 264.93, 251.46, 241.27, 222.98, 203.73, 184.1, 166.12, 138.71, 119.71, 100.41, 79.76, 50.62, 32.99, 2.14]代码:
import matplotlib.pyplot as plt
from numpy import *
dt = 0.5
# 状态转移矩阵F0
F = mat([[1, dt, dt * dt / 2, 0, 0, 0],
[0, 1, dt, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, dt, dt * dt / 2],
[0, 0, 0, 0, 1, dt],
[0, 0, 0, 0, 0, 1]])
# 过程噪声(协方差)矩阵
Q = mat([[pow(dt, 4) / 4, pow(dt, 3) / 2, pow(dt, 2) / 2, 0, 0, 0],
[pow(dt, 3) / 2, pow(dt, 2), dt, 0, 0, 0],
[pow(dt, 2) / 2, dt, 1, 0, 0, 0],
[0, 0, 0, pow(dt, 4) / 4, pow(dt, 3) / 2, pow(dt, 2) / 2],
[0, 0, 0, pow(dt, 3) / 2, pow(dt, 2), dt],
[0, 0, 0, pow(dt, 2) / 2, dt, 1]])
# 测量不确定性(协方差)矩阵
Rn = mat([[9, 0],
[0, 9]])
# 观测矩阵
H = mat([[1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0]])
# 测量值
x = []
y = []
# 估计值
xe = []
ye = []
# 真实值
xt = []
yt = []
# 系统状态向量
sn = mat([0, 0, 0, 0, 0, 0]).T
# 卡尔曼增益
Pn = mat([[500, 0, 0, 0, 0, 0],
[0, 500, 0, 0, 0, 0],
[0, 0, 500, 0, 0, 0],
[0, 0, 0, 500, 0, 0],
[0, 0, 0, 0, 500, 0],
[0, 0, 0, 0, 0, 500]])
# 初始化
Pn = F @ Pn @ F.T + Q
sn = F * sn
# 存储
se = []
P = []
def kalman_filter():
global Pn, sn
for i in range(0, len(x)):
# 测量值
z = mat([x[i], y[i]]).T
# 估计卡尔曼增益
Kn = Pn @ H.T @ (H @ Pn @ H.T + Rn).I
# 估计系统状态
sen = sn + Kn @ (z - H @ sn)
se.append(sen)
xe.append(float(sen[0]))
ye.append(float(sen[3]))
Id = identity(6)
# 更新当前估计不确定性
Pe = (Id - Kn @ H) @ Pn @ (Id - Kn @ H).T + Kn @ Rn @ Kn.T
# 预测估计不确定性
Pn = F @ Pe @ F.T + Q
# 预测下次系统状态
sn = F * sen
if __name__ == '__main__':
x = [-393.66, -375.93, -351.04, -328.96, -299.35, -273.36, -245.89, -222.58, -198.03, -174.17, -146.32, -123.72,
-103.47, -78.23, -52.63, -23.34, 25.96, 49.72, 76.94, 95.38, 119.83, 144.01, 161.84, 180.56, 201.42, 222.62,
239.4, 252.51, 266.26, 271.75, 277.4, 294.12, 301.23, 291.8, 299.89]
y = [300.4, 301.78, 295.1, 305.19, 301.06, 302.05, 300, 303.57, 296.33, 297.65, 297.41, 299.61, 299.6, 302.39,
295.04, 300.09, 294.72, 298.61, 294.64, 284.88, 272.82, 264.93, 251.46, 241.27, 222.98, 203.73, 184.1, 166.12,
138.71, 119.71, 100.41, 79.76, 50.62, 32.99, 2.14]
xt = linspace(-400, 300, 35)
yt = repeat(300, 35)
for i in range(20, 35):
yt[i] = sqrt(300 * 300 - xt[i] * xt[i])
kalman_filter()
plt.plot(xt, yt, label="True value")
plt.plot(x, y, label="Measurements", marker='o')
plt.plot(xe, ye, label="Estimates", marker='o')
plt.grid(linestyle='--')
plt.xlabel("X(m)")
plt.ylabel("Y(m)")
plt.legend(loc='lower left')
plt.show()
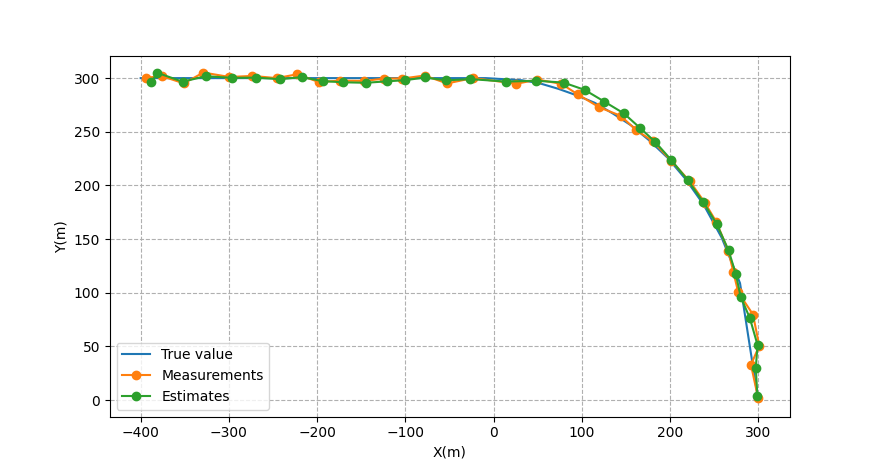
得到结果
总结
卡尔曼滤波跟踪车辆的效果很好,但是在车辆开始转弯时,估计不准确,过了一段时间趋于准确。
角加速度$\alpha=\frac{\Delta V}{R \Delta t}$。
虽然角加速度恒定,角加速度投影到$x$和$y$轴上不恒定,所以$\ddot{x}$和$\ddot{y}$不为常数。
这个卡尔曼滤波器为恒定加速度模型,最终在选择正确的$\sigma_a^2$参数使得跟踪转弯车辆成功。
可以尝试改变$\sigma_a^2$来测试不同的情况。
例子10-火箭高度估计
加速度作为控制输入
考虑常加速度动态系统
加速计不感应重力。在桌子上静止的加速度计将向上测量1g,而自由落体的加速度计将测量0。因此,我们需要从每个加速度计的测量中减去重力加速度常数g。
在时间步骤1g的加速度计测量值为:
$$ a_{n} = \ddot{x} - g + \epsilon $$其中:
- $\ddot{x}$ 为实际的物体加速度
- $g$ 为重力加速度常数;$g=9.8m/s$
- $\epsilon$ 为加速度测量误差
状态外推方程
一般形式:
$$ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_n+w_n} $$其中: $\boldsymbol{\hat{x}_{n+1,n} }$ 为时间为$n+1$时预测系统状态向量 $\boldsymbol{\hat{x}_{n,n} }$ 为时间为$n$时系统状态向量 $\boldsymbol{u_n}$ 为控制变量或者输入变量-对系统的可测量的(确定性的)输入 $\boldsymbol{w_n}$ 为过程噪声或干扰–影响状态的不可测量的输入 $\boldsymbol{F}$ 为系统转移矩阵 $\boldsymbol{G}$ 为控制矩阵或输入转换矩阵(将控制变量映射到状态变量)
该例子中有控制变量$u$,基于加速度测量值
系统状态定义为$\boldsymbol{x}_n$:
$$ \boldsymbol{x}_n=\begin{bmatrix} x_n \\ \dot{x}_n \end{bmatrix} $$其中
- $x_n$ 为时间为n时的火箭高度
- $\boldsymbol{\dot{x}_n}$ 为时间为n时的火箭速度
状态外推方程如下:
$$ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{\dot{x}}_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{\dot{x}}_{n,n}\\ \end{matrix} \right] + \left[ \begin{matrix} 0.5 \Delta t^{2} \\ \Delta t \\ \end{matrix} \right] \left( a_{n} + g \right) $$其中:
$$ \boldsymbol{F}= \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] $$$$ \boldsymbol{G}= \left[ \begin{matrix} 0.5 \Delta t^{2} \\ \Delta t \\ \end{matrix} \right] $$$$ \boldsymbol{u_{n}}= \left( a_{n} + g \right) $$协方差外推方程
一般形式:
$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$其中 $\boldsymbol{P_{n,n} }$ 为估计不确定性 $\boldsymbol{P_{n+1,n} }$ 为预测不确定性 $\boldsymbol{F}$ 为“线性动态系统建模”一节中得出的状态转换矩阵 $\boldsymbol Q$ 为过程噪声矩阵
估计不确定性矩阵形式为:
$$ \boldsymbol{P} = \left[ \begin{matrix} p_{x} & p_{x\dot{x}} \\ p_{\dot{x}x} & p_{\dot{x}} \\ \end{matrix} \right] $$分别对应位置和速度的不确定性
过程噪声矩阵
只有高度和速度两个系统状态变量,所以噪声矩阵为
$$ \boldsymbol{Q} = \left[ \begin{matrix} \sigma_{x}^{2} & \sigma_{x\dot{x}}^{2} \\ \sigma_{\dot{x}x}^{2} & \sigma_{\dot{x}}^{2} \\ \end{matrix} \right] $$根据恒定加速度模型里面推导的噪声矩阵为:
$$ \boldsymbol{Q} = \left[ \begin{matrix} \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} \\ \frac{\Delta t^{3}}{2} & \Delta t^{2} \\ \end{matrix} \right] \epsilon^{2} $$$$ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} $$$$ \left[ \begin{matrix} p_{x_{n+1,n}} & p_{x\dot{x}_{n+1,n}} \\ p_{\dot{x}x_{n+1,n}} & p_{\dot{x}_{n+1,n}} \\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] \times \left[ \begin{matrix} p_{x_{n,n}} & p_{x\dot{x}_{n,n}} \\ p_{\dot{x}x_{n,n}} & p_{\dot{x}_{n,n}} \\ \end{matrix} \right] \times \left[ \begin{matrix} 1 & 0 \\ \Delta t & 1 \\ \end{matrix} \right] + \left[ \begin{matrix} \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} \\ \frac{\Delta t^{3}}{2} & \Delta t^{2} \\ \end{matrix} \right] \epsilon^{2} $$测量方程
一般的测量方程为:
一般形式如下:
$$ \boldsymbol{z_{n} = Hx_{n} + v_{n} } $$$\boldsymbol z_n$ 为测量值向量 $\boldsymbol x_n$ 为真实系统状态 $\boldsymbol v_n$ 为随机噪声向量 $\boldsymbol H$ 为观测矩阵
测量值仅有火箭的高度:$\boldsymbol{z_{n}} = \left[ x_{n,measured} \right]$
$$ \boldsymbol{z_{n} = Hx_{n}} $$$$ \left[ x_{n,measured} \right] = \boldsymbol{H} \left[ \begin{matrix} x_{n}\\ \dot{x}_{n} \\ \end{matrix} \right] $$二维变为一维:
$$ \boldsymbol{H}=\begin{bmatrix} 1 & 0 \end{bmatrix} $$测量不确定性
测量协方差矩阵为:
$$ \boldsymbol{R_{n}} = \left[ \sigma_{x_{m}}^{2} \right] $$简化测量不确定性,每次测量都是一样
$$ \boldsymbol{R_{1}} = \boldsymbol{R_{2}} ... \boldsymbol{R_{n-1}} = \boldsymbol{R_{n}} = \boldsymbol{R} $$卡尔曼增益
一般形式:
$$ \boldsymbol{ K_{n} = P_{n,n-1}H^{T}\left( HP_{n,n-1}H^{T} + R_{n} \right)^{-1} } $$其中: $\boldsymbol{K_n}$ 为卡尔曼增益 $\boldsymbol{P_{n,n-1} }$ 为之前的估计不确定性(协方差)矩阵对当前状态的预测 $\boldsymbol{H}$ 为观测矩阵 $\boldsymbol{R_n}$ 为测量不确定性(测量噪声协方差矩阵)
根据已经推导的结果:
$$ \left[ \begin{matrix} K_{1,1_{n}} \\ K_{2,1_{n}} \\ \end{matrix} \right] = \left[ \begin{matrix} p_{x_{n,n-1}} & p_{x\dot{x}_{n,n-1}} \\ p_{\dot{x}x_{n,n-1}} & p_{\dot{x}_{n,n-1}} \\ \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right] \times \left( \left[ \begin{matrix} 1 & 0 \\ \end{matrix}\right] \left[ \begin{matrix} p_{x_{n,n-1}} & p_{x\dot{x}_{n,n-1}} \\ p_{\dot{x}x_{n,n-1}} & p_{\dot{x}_{n,n-1}} \\ \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ \end{matrix} \right] + \left[ \sigma_{x_{m}}^{2} \right] \right)^{-1} $$状态更新方程
状态更新方程的形式为:
$$ \boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )} $$其中: $\boldsymbol{\hat{x}_{n,n} }$ 为时间为n时的估计系统状态向量 $\boldsymbol{\hat{x}_{n,n-1} }$ 为时间为n-1时的预测系统状态向量 $\boldsymbol {H_n}$ 为卡尔曼增益 $\boldsymbol {z_n}$为测量值 $\boldsymbol {H}$ 为观测矩阵
协方差更新方程
$$ \boldsymbol{ P_{n,n} = \left( I - K_{n}H \right) P_{n,n-1} \left( I - K_{n}H \right)^{T} + K_{n}R_{n}K_{n}^{T} } $$其中: $\boldsymbol{P_{n,n} }$ 估计不确定性(协方差)矩阵当前状态 $\boldsymbol{P_{n,n-1} }$ 之前估计不确定性(协方差)矩阵对于当前状态的预测 $\boldsymbol K_n$ 卡尔曼增益 $\boldsymbol H$ 观测矩阵 $\boldsymbol R_n$ 测量不确定性(测量噪声协方差矩阵)
数值例子
假设火箭垂直向上发射,加速度不变
- 测量间隔:$\Delta t=0.25s$
- 火箭加速度:$\ddot x=30m/s^2$
- 高度测量标准差:$\sigma_{x_m}=20m$
- 加速度测量标准差:$\epsilon=0.1m/s^2$
- 状态转移矩阵$\boldsymbol F$为:
- 控制矩阵$\boldsymbol G$为:
- 过程噪声矩阵$\boldsymbol Q$为:
- 测量不确定性$\boldsymbol R$为:
测量值为:
xn = [-32.4, -11.1, 18, 22.9, 19.5, 28.5, 46.5, 68.9, 48.2, 56.1, 90.5, 104.9, 140.9, 148, 187.6, 209.2, 244.6, 276.4, 323.5, 357.3, 357.4, 398.3, 446.7, 465.1, 529.4, 570.4, 636.8, 693.3, 707.3, 748.5]
an = [39.72, 40.02, 39.97, 39.81, 39.75, 39.6, 39.77, 39.83, 39.73, 39.87, 39.81, 39.92, 39.78, 39.98, 39.76, 39.86, 39.61, 39.86, 39.74, 39.87, 39.63, 39.67, 39.96, 39.8, 39.89, 39.85, 39.9, 39.81, 39.81, 39.68]代码:
import matplotlib.pyplot as plt
from numpy import *
dt = 0.25
# 状态转移矩阵F0
F = mat([[1, dt],
[0, 1]])
# 控制矩阵
G = mat([[0.5 * dt * dt],
[dt]])
# 过程噪声(协方差)矩阵
Q = mat([[pow(dt, 4) / 4, pow(dt, 3) / 2],
[pow(dt, 3) / 2, pow(dt, 2)]])
# 测量不确定性(协方差)矩阵
Rn = mat([[400]])
# 观测矩阵
H = mat([[1, 0]])
# 测量值
x = []
a = []
# 估计值
xe = []
ae = []
# 真实值
xt = []
at = []
# 系统状态向量
sn = mat([0, 0]).T
# 控制输入
un = 0
# 卡尔曼增益
Pn = mat([[500, 0],
[0, 500]])
# 初始化
Pn = F @ Pn @ F.T + Q
sn = F * sn + G * un
# 存储
se = []
P = []
def kalman_filter():
global Pn, sn, un
for i in range(0, len(x)):
# 测量值
z = mat([x[i]]).T
# 估计卡尔曼增益
Kn = Pn @ H.T @ (H @ Pn @ H.T + Rn).I
P.append(float(Kn[0]))
# 估计系统状态
sen = sn + Kn @ (z - H @ sn)
se.append(sen)
xe.append(float(sen[0]))
ae.append(float(sen[1]))
Id = identity(2)
# 更新当前估计不确定性
Pe = (Id - Kn @ H) @ Pn @ (Id - Kn @ H).T + Kn @ Rn @ Kn.T
# 预测估计不确定性
Pn = F @ Pe @ F.T + Q
# 预测下次系统状态
un = a[i]
sn = F * sen + G * un
if __name__ == '__main__':
x = [-32.4, -11.1, 18, 22.9, 19.5, 28.5, 46.5, 68.9, 48.2, 56.1, 90.5, 104.9, 140.9, 148, 187.6, 209.2, 244.6,
276.4, 323.5, 357.3, 357.4, 398.3, 446.7, 465.1, 529.4, 570.4, 636.8, 693.3, 707.3, 748.5]
a = [39.72, 40.02, 39.97, 39.81, 39.75, 39.6, 39.77, 39.83, 39.73, 39.87, 39.81, 39.92, 39.78, 39.98, 39.76, 39.86,
39.61, 39.86, 39.74, 39.87, 39.63, 39.67, 39.96, 39.8, 39.89, 39.85, 39.9, 39.81, 39.81, 39.68]
t = linspace(0, len(x) * dt, len(x))
xt = 30 / 2 * t * t
kalman_filter()
plt.plot(t, xt, label="True value")
plt.plot(t, x, label="Measurements", marker='o')
plt.plot(t, xe, label="Estimates", marker='o')
plt.grid(linestyle='--')
plt.xlabel("t(s)")
plt.ylabel("h(m)")
plt.legend(loc='upper left')
plt.figure()
plt.plot(t, P)
plt.title("Kalman Gain")
plt.xlabel("t(s)")
plt.ylabel("Kalman Gain")
plt.grid(linestyle='--')
plt.show()
得到结果
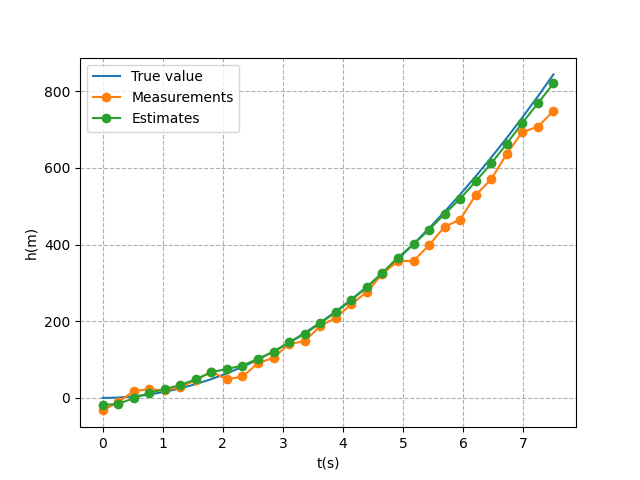
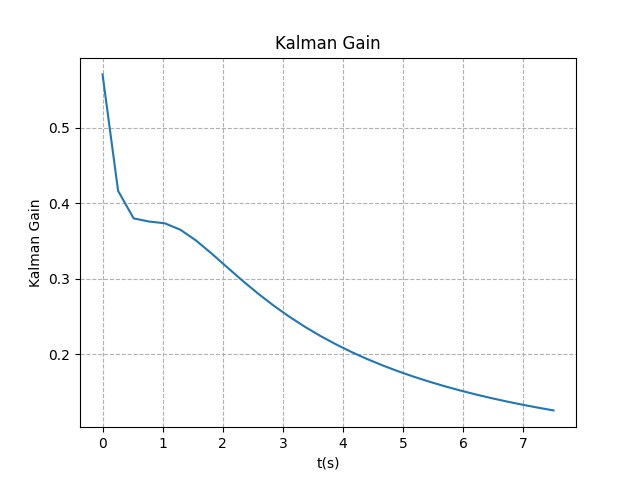
一开始估计的高度受测量值影响,没有和真实值对齐,测量值噪声很大。
但随着卡尔曼增益的收敛,噪声测量的影响越来越小,估计的高度与真实高度很一致。
在这个例子中,我们没有任何导致加速度变化的操纵,但如果我们有,控制输入(加速度计)将更新状态外推方程。
下一步是什么
下面的列表包含了未来的主题。其中一些是深入理解卡尔曼滤波的必要条件。
- 卡尔曼滤波的初始化
- 扩展卡尔曼滤波(卡尔曼滤波的非线性版本)
- 无色的卡尔曼滤波
- 非高斯噪声卡尔曼滤波(当噪声分布为非高斯时,如何泛化卡尔曼滤波)
- 稳定性和发散性(如何设计不发散的稳定卡尔曼滤波器)
- 次优滤波(如何处理测量不确定性高于预期的情况)
- 简化卡尔曼滤波,提高计算性能
- 卡尔曼滤波的实现
更多资料
卡尔曼滤波Python形式:
https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python