说明
原教程英文网址:扩展卡尔曼滤波
实际应用
当以下情况出现时非常有用:
- 机器人传感器感知世界
- 机器人传感器不是100%准确
把传感器观测值通过EKF,可以平滑噪声计算出每个时刻更好的估计值
先决条件
需要了解状态空间模型和观测模型。对于EKF来说是两个主要组成部分。
可以参考之前的博客:卡尔曼滤波
卡尔曼滤波和扩展卡尔曼滤波区别
卡尔曼滤波只适用于现行系统,扩展卡尔曼滤波可以用于非线性系统,比如移动机器人
例如卡尔曼滤波该形式下不能用(其中\(\gamma\)为偏航角yaw):
\[ \begin{bmatrix} x_t\\ y_t\\ \gamma_t \end{bmatrix} = \begin{bmatrix} x_{t-1}+v_{t-1}\cos{\gamma_{t-1}}*dt\\ y_{t-1}+v_{t-1}\sin{\gamma_{t-1}}*dt\\ \gamma_{t-1}+\omega_{t-1}*dt \end{bmatrix} = \begin{bmatrix} f_1\\ f_2\\ f_3 \end{bmatrix} \]
如果方程为该形式则可以:
\[ \begin{bmatrix} x_t\\ y_t\\ \gamma_t \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} x_{t-1}\\ y_{t-1}\\ \gamma_{t-1} \end{bmatrix}+ \begin{bmatrix} \cos{\gamma_{t-1}}*dt & 0\\ \sin{\gamma_{t-1}}*dt & 0\\ 0&dt \end{bmatrix} \begin{bmatrix} v_{t-1}\\ \omega_{t-1} \end{bmatrix}+ \begin{bmatrix} noise_{t-1}\\ noise_{t-1}\\ noise_{t-1} \end{bmatrix} \]
另外一个例子,考虑以下方程:
\[ 下一次状态=4\times(当前状态)+3 \]
该方程为线性系统,常规卡尔曼滤波可以使用
但是对于以下方程:
\[ 下一次状态=当前状态+17\times \cos(当前状态) \]
该方程为非线性。我们需要对其线性化。当我们放大曲线后,放得越大线条越接近直线。在扩展卡尔曼滤波中,我们把非线性方程通过雅可比矩阵(Jacobian)转化成线性。
雅可比矩阵是函数一阶偏导数以一定方式排列成的矩阵,假设\(\mathbb{R}_n\rightarrow \mathbb{R_m}\)表示函数映射,函数由m个实函数组成
\[ y_1(x_1,\dots,x_n),\dots,y_m(x_1,\dots,x_n) \]
偏导数矩阵为:
\[ \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \dots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \dots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \]
扩展卡尔曼滤波假设
假设已经推导了两个关键数学方程:
EKF算法
站在高的角度看,EKF算法有两步,预测和更新(纠正),和一般卡尔曼滤波一样
预测步骤
- 使用状态空间模型,使用t-1时刻的估计值(通过t-1时刻的控制量得到的)预测t时刻的系统状态
- 通过协方差外推方程根据之前的协方差和噪声
更新步骤
- 计算时间t的实际传感器测量值减去测量模型预测的当前时间步长t的传感器测量值的差
- 计算测量残留协方差
- 计算接近最佳的卡尔曼增益
- 计算t时刻的状态估计值
- 更新t时刻的状态协方差估计
一步一步
机器人在\(xy\)平面移动,有\(x,y,\gamma\)分别代表\(x,y\)位置和航向角yaw,输入控制变量为线速度\(v\)和角速度\(\omega\),由于系统状态向量用\(\boldsymbol {\hat x}\)表示,所以\(x\)轴的位置用\(p\)代替,时间\(t\)用\(n\)代替
卡尔曼方程
状态外推方程
\[ \boldsymbol{\hat{x}_{n+1,n}=F\hat{x}_{n,n}+Gu_n+w_n} \]
在该例子中,系统状态变量为
\[ \hat x_n = \begin{bmatrix} p_n\\ y_n\\ \gamma_n \end{bmatrix} \]
输入控制量为:
\[ \boldsymbol{u_n}=\begin{bmatrix} v_n\\ \omega_n \end{bmatrix} \]
计算系统转移矩阵
\[ \begin{array}{c} p_n=p_{n-1}+v_{n-1}\Delta t\cos(\gamma_{n-1})\\ y_n=y_{n-1}+v_{n-1}\Delta t\sin(\gamma_{n-1})\\ \gamma_n = \gamma_{n-1} + \omega_{n-1}\Delta t \end{array} \]
整理成矩阵形式:
\[ \boldsymbol{\hat x_n}=\begin{bmatrix} p_n\\ y_n\\ \gamma_n \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} p_{n-1}\\ y_{n-1}\\ \gamma_{n-1} \end{bmatrix}+ \begin{bmatrix} \cos(\gamma_{n-1})\Delta t&0\\ \sin(\gamma_{n-1})\Delta t&0\\ 0 &\Delta t \end{bmatrix} \begin{bmatrix} v_{k-1}\\ \omega_{k-1} \end{bmatrix}+\boldsymbol{w_n} \]
\[ \boldsymbol {F}=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \]
\[ \boldsymbol G =\begin{bmatrix} \cos(\gamma_{n-1})\Delta t&0\\ \sin(\gamma_{n-1})\Delta t&0\\ 0 &\Delta t \end{bmatrix} \]
协方差外推方程
\[ \boldsymbol{P_{n+1,n} = FP_{n,n}F^{T} + Q} \]
\[ \boldsymbol Q=\begin{bmatrix} V(p)&COV(p,y)&COV(p,\gamma)\\ COV(y,p)&V(y)&COV(y,\gamma)\\ COV(\gamma,p)&COV(\gamma,y)&V(\gamma) \end{bmatrix} \]
考虑到系统状态变量的相关性
\[ \boldsymbol Q=\begin{bmatrix} V(p)&0&0\\ 0&V(y)&0\\ 0&0&V(\gamma) \end{bmatrix} \]
测量方程
\[ \boldsymbol{z_{n} = Hx_{n} + v_{n} } \]
假设不存在测量噪声
\[ \boldsymbol H = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \]
测量不确定性
假设
\[ \boldsymbol{R_{1}} = \boldsymbol{R_{2}} ... \boldsymbol{R_{n-1}} = \boldsymbol{R_{n}} = \boldsymbol{R} \]
数值例子
初始状态估计协方差
\[ \boldsymbol P =\begin{bmatrix} 0.1&0&0\\ 0&0.1&0\\ 0&0&0.1 \end{bmatrix} \]
过程噪声
\[ \boldsymbol{w_n} = \begin{bmatrix} 0.07\\ 0.07\\ 0.04 \end{bmatrix} \]
过程噪声矩阵 \[ \boldsymbol Q = \begin{bmatrix} 0.01&0&0\\ 0&0.01&0\\ 0&0&0.01 \end{bmatrix} \]
上面已经得到
1. 初始化
初始统状态设置为:
\[ \boldsymbol{x_0}=\begin{bmatrix} x_t\\ y_t\\ \gamma_t \end{bmatrix} =\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} \]
初始控制输入线速度和角速度为:
\[ \boldsymbol{u_0}=\begin{bmatrix} v_{k-1}\\ w_{k-1} \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \]
2. 预测状态估计
使用状态外推方程
3. 预测协方差状态估计
使用协方差外推方程
4. 估计系统状态
使用状态更新方程
\[ \boldsymbol{\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_{n} ( z_{n} - H \hat{x}_{n,n-1} )} \]
5. 更新协方差
使用协方差更新方程
\[ \boldsymbol{ P_{n,n} = \left( I - K_{n}H \right) P_{n,n-1} \left( I - K_{n}H \right)^{T} + K_{n}R_{n}K_{n}^{T} } \]
6. 近似最优卡尔曼增益
…
使用匀速圆周运动模拟数据
代码:
import matplotlib.pyplot as plt
from numpy import *
import random
dt = 0.5
F = mat([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
# G 为非线性
# G =
Q = mat([[0.01, 0, 0],
[0, 0.01, 0],
[0, 0, 0.01]])
# 测量不确定性
Rn = mat([[0.1, 0, 0],
[0, 0.1, 0],
[0, 0, 0.1]])
# 观测矩阵
H = mat([[1.0, 0, 0],
[0, 1.0, 0],
[0, 0, 1.0]])
# 过程噪声
w = mat([[0.01, 0.01, 0.003]]).T
# 测量值
x = []
y = []
yaw = []
# 估计值
xe = []
ye = []
yawe = []
# 真实值
xt = []
yt = []
yawt = []
xp = []
yp = []
yawp = []
# 系统状态向量
sn = mat([[10, 0, 0]]).T
# 控制输入
u = []
# 卡尔曼增益
Pn = mat([[500, 0, 0],
[0, 500, 0],
[0, 0, 500]])
# 初始化
# Pn = F @ Pn @ F.T + Q
# sn = F * sn + G * un
# 存储
se = []
K = []
def update_sn(s, u):
G = mat([[math.cos(s[2][0] / 180 * pi) * dt, 0],
[math.sin(s[2][0] / 180 * pi) * dt, 0],
[0, dt]])
return F * s + G * u
def ekf():
global Pn, sn
for index in range(0, len(x)):
# 测量值
z = mat([x[index], y[index], yaw[index]]).T
# 估计卡尔曼增益
Kn = Pn @ H.T @ (H @ Pn @ H.T + Rn).I
K.append(array(Kn[0])[0])
print(Kn)
# 估计系统状态
sen = sn + Kn @ (z - H @ sn)
se.append(sen)
xe.append(float(sen[0]))
ye.append(float(sen[1]))
yawe.append(float(sen[2]))
Id = identity(3)
# 更新当前估计不确定性
Pe = (Id - Kn @ H) @ Pn @ (Id - Kn @ H).T + Kn @ Rn @ Kn.T
# 预测估计不确定性
Pn = F @ Pe @ F.T + Q
# 预测下次系统状态
un = u[index]
sn = update_sn(sen, un)
xp.append(float(sen[0]))
yp.append(float(sen[1]))
yawp.append(float(sen[2]))
if __name__ == '__main__':
# 匀速圆周运动
time = []
for i in range(0, 20):
time.append(i * dt)
R = 10
omega = 90 / 20 / dt
theta = omega * i * dt
xt_n = R * math.cos(theta / 180 * pi)
yt_n = R * math.sin(theta / 180 * pi)
yaw_n = 90 + theta
u.append(mat([[omega / 180 * pi * R], [omega]]))
xt.append(xt_n)
yt.append(yt_n)
yawt.append(yaw_n)
x.append(xt_n + random.uniform(-0.5, 0.5))
y.append(yt_n + random.uniform(-0.5, 0.5))
yaw.append(yaw_n + random.uniform(-1, 1))
sn = update_sn(sn, mat([0, 0]).T)
Pn = F @ Pn @ F.T + Q
ekf()
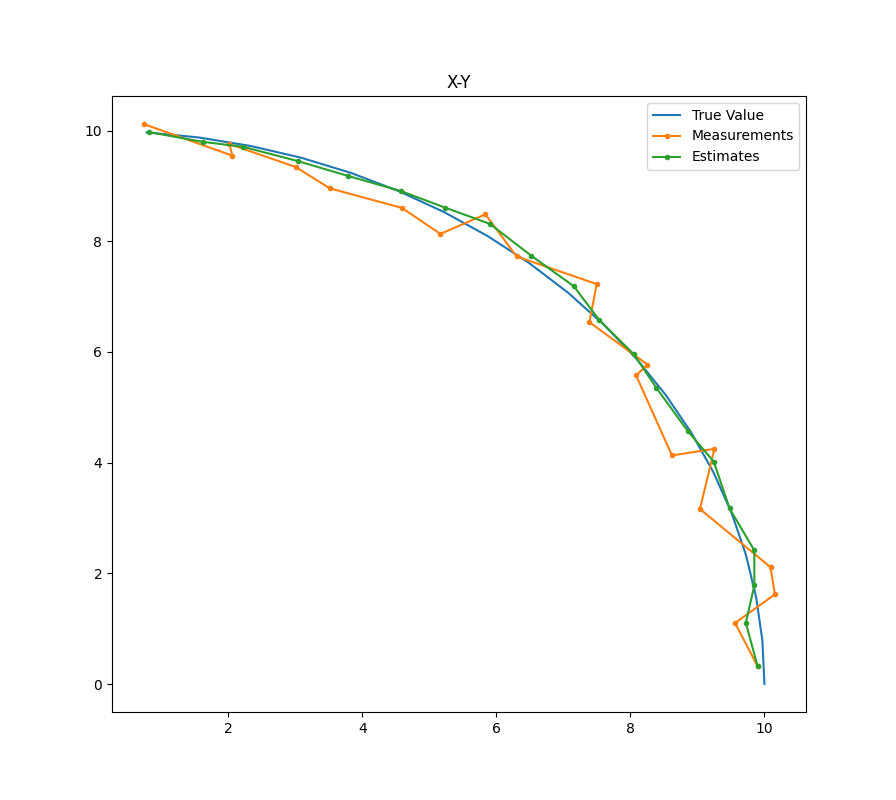
plt.title("X-Y")
plt.plot(xt, yt, label="True Value")
plt.plot(x, y, label="Measurements", marker='.')
plt.plot(xe, ye, label="Estimates", marker='.')
# plt.plot(xp, yp, label="Predict", marker='.')
# plt.plot(x, predict_pos, label="Predict", marker='^')
plt.legend(loc='upper right')
plt.figure()
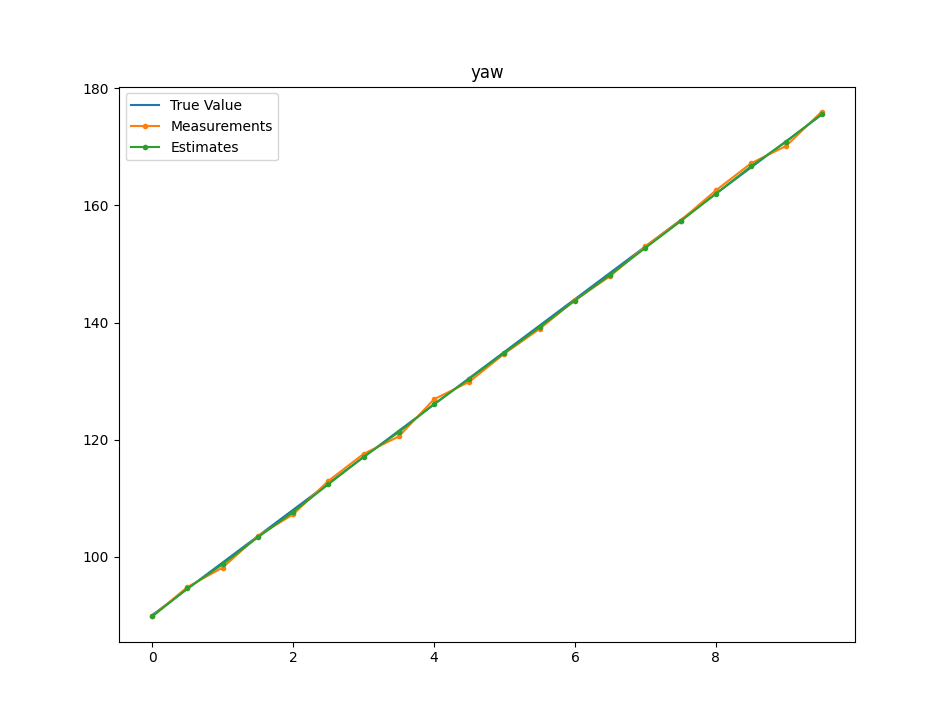
plt.title("yaw")
plt.plot(time, yawt, label="True Value")
plt.plot(time, yaw, label="Measurements", marker='.')
plt.plot(time, yawe, label="Estimates", marker='.')
plt.legend(loc='upper left')
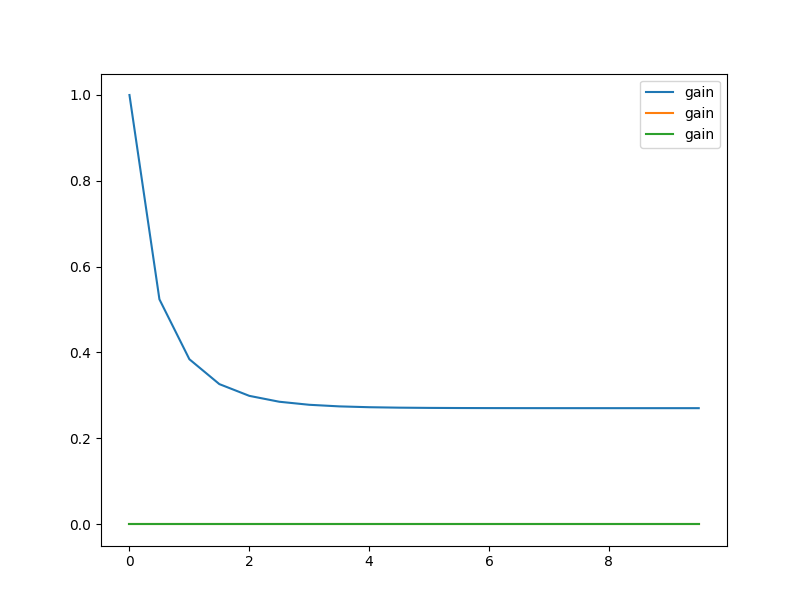
plt.figure()
plt.plot(time, K, label="gain")
plt.legend(loc='upper right')
plt.show()
结果: