LIO-SAM论文阅读

LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping

介绍

状态估计、定位和建图对于成功的智能移动机器人来说是必备的，需要反馈控制、避障、规划路线和其他能力。使用视觉的和激光的传感器，为了实现高性能实时同时定位和建图（SLAM）使得移动机器人支持6自由度状态估计，投入了很大的精力。基于视觉的方案通常使用双目或立体相机，对连续的图像进行三角定位，以确定像机的运动。虽然基于视觉的方案对于位置识别更加合适，但是它们对初始化、光照和范围的敏感性使它们在单独用于支持自主导航系统时不可靠。另一方面，基于激光的方案大体上不受光照变化的影响。尤其是最近有远距离，高解析度的3D雷达可供选择，比如Velodyne VLS-128和Ouster OS1-128，雷达更适合在三维空间中直接获取环境信息。

在过去的20年里面，很多人提出了很多基于雷达状态估计和建图方法。其中雷达里程计和建图（LOAM）方法以其低漂移和实时状态估计建图被广泛应用¹。LOAM使用激光雷达和惯性测量单元（IMU），实现了KITTI里程计跑分登顶²。除了LOAM的成功，它也表现出一些限制——由于保存数据在一个全局的点云地图里面，很难实现回环检测和插入其他绝对测量值，比如GPS来纠正位置。在富含特征的环境中由于点云地图过大它的在线优化过程效率很低。LOAM也在大地图规模测试中受到漂移的影响，由于它是基于扫描-匹配的方法。

在该论文中，我们推出一个紧耦合通过平滑和建图的雷达惯性里程计框架，LIO-SAM，以解决上述问题。我们假设使用非线性运动模型点云去畸变、使用原始IMU数据在雷达扫描期间估计传感器运动。为了对点云去畸变，估计的运动可以作为激光雷达里程计优化的初始猜测。获得的激光雷达里程计的结果用于在因子图中估计IMU偏差。通过引入全局因子图估计机器人航迹，我们可以更有效的实现激光雷达和IMU传感器的融合、在机器人的姿态中加入地点识别和引入绝对位置测量例如GPS坐标和罗盘角度，如果允许。这些来自不同来源的因子的集合用来做图优化。此外，我们将旧的激光雷达扫描边缘化，以进行姿势优化，而不是像LOAM那样将扫描与全局地图相匹配。在局部范围而不是全局范围的扫描匹配大大改善了系统的实时性能，有选择地引入关键帧和有效的滑动窗口方法也是如此，该方法将一个新的关键帧注册到一个固定大小的先前 “子关键帧 “集合中。我们工作的主要成果总结如下：

• 一种基于因子图构建的紧耦合雷达惯性里程计框架，适合多传感器融合和全局优化
• 一种高效的、基于局部滑动窗口的扫描匹配方法，通过将有选择地选择的新关键帧注册到固定大小的先前子关键帧集上，实现实时性能。
• 所提出的框架得到了广泛的验证。在各种规模、车辆和环境中进行测试，广泛验证了所提出的框架。

相关工作

激光雷达里程计通常是通过使用扫描-匹配方法（如ICP³和GICP⁴）找到两个连续帧之间的相对变换来进行的。基于特征的匹配由于其计算性能效率越来越流行了。两个例子，飞机对准⁵和海岸线对齐⁶

因此，激光雷达通常与其他传感器（如IMU和GPS）一起使用，用于状态估计和建图。这种利用传感器融合的设计方案，通常可以分为两类：松耦合融合和紧耦合融合。在LOAM中¹，引入了IMU来对激光雷达扫描数据进行去畸变，并为扫描匹配提供运动先验。然而，IMU并没有参与优化过程算法。所以LOAM可以归为松耦合方法。LeGO-LOAM⁷提出为地面车辆建图⁸。它融合IMU测量数据和LOAM一样。更流行的松耦合融合方法是使用扩展卡尔曼滤波（EKF）。例如^910111213，使用雷达、IMU和可选的GPS使用EKF优化机器人状态估计。

紧密耦合的系统通常能提供更好的精度，目前是正在进行的研究的一个主要焦点¹⁴。在¹⁵中，IMU测量值预积分被利用于点云去畸变。一个以机器人为中心的激光雷达-惯性状态估计器，LINS在¹⁶中。为地面车辆设计，使用错误状态卡尔曼滤波纠正机器人状态估计，以一种紧耦合的方式迭代。LIOM¹⁷，LIO-mapping的缩写，结合优化激光雷达和IMU数据实现比LOAM相似或者更准确的效果。由于LIOM是设计处理所有传感器测量数据，实时性能没有实现——测试中只运行了0.6倍实时性。

LIO-SAM

A. 系统组成

首先定义术语和符号。世界框架为$\mathbf{W}$，机器人主体框架为$\mathbf{B}$。为方便起见，我们还假设IMU框架与机器人主体框架相吻合。机器人状态$x$可以写为：

$$ \mathbf{x}=\left[\mathbf{R}^{\text{T}},\mathbf{p}^{\text{T}},\mathbf{v}^{\text{T}},\mathbf{b}^{\text{T}}\right]^{\text{T}} $$

其中$\mathbf{R}\in SO(3)$为旋转矩阵，$\mathbf{p}\in \mathbb{R}^3$为位置向量，$\mathbf{v}$为速度，$\mathbf{b}$为IMU偏差，从$\mathbf B$到$\mathbf W$的变换$\mathbf{T}\in SE(3)$表示为$\mathbf{T}=[\mathbf{R}|\mathbf{p}]$

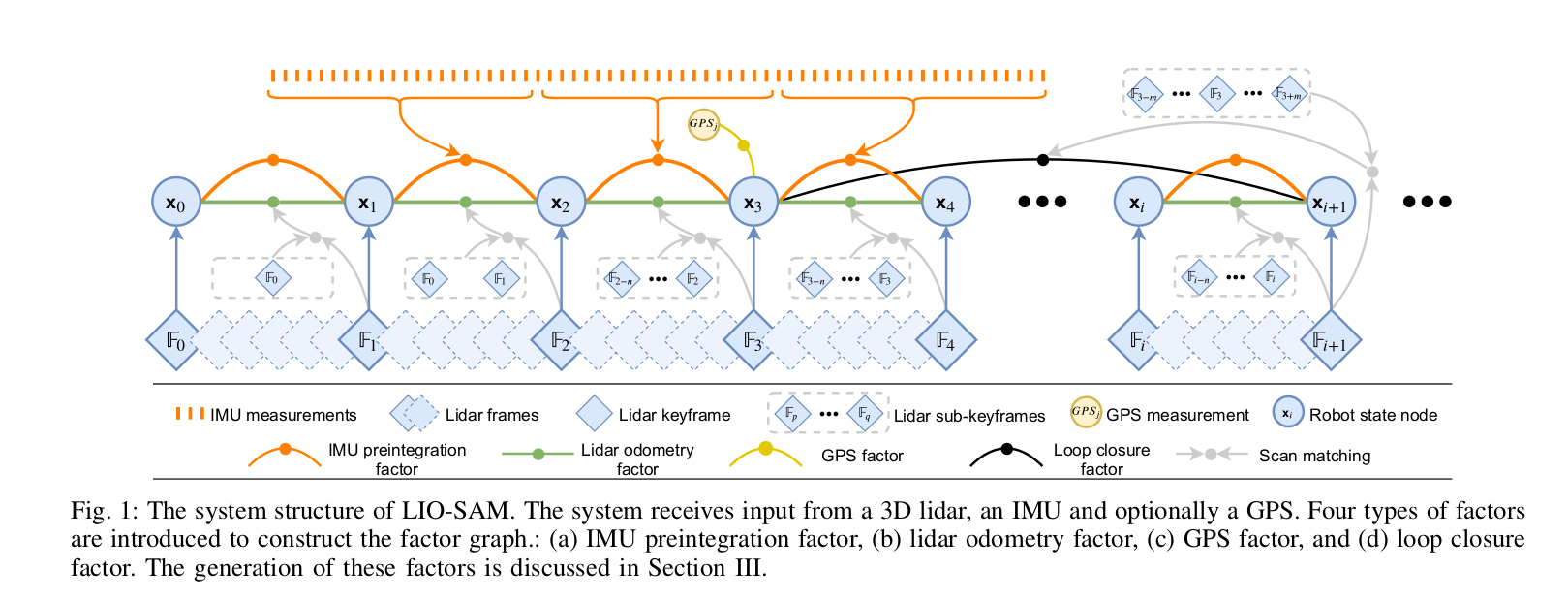
系统的总览图见上图。系统从3D激光雷达、IMU和可选的GPS接收数据。我们通过这些传感器的观测值来估计机器人状态和航迹。这个状态估计问题可以被表述为一个最大后验（MAP）问题。我们使用因子图建模表示该问题，因为与贝叶斯网相比，它更适合进行推理。假设一个高斯噪声模型，该问题等效为解决一个非线性最小二乘法问题¹⁸。请注意，在不丧失一般性的情况下，所提议的系统也可以纳入来自其他传感器的测量，如来自高度计的海拔高度或来自罗盘的方向。

我们引入了四种类型的因子和一种变量类型来构建因子图。该变量代表特定时刻机器人状态，为图中节点的属性。四种类型的因子分别为：(a) IMU预积分因子，(b) 激光雷达里程计因子，(c) GPS因子和 (d) 回环因子。当机器人位置超过用户定义的阈值，新的状态节点$\mathbf{x}$添加到图中。在插入一个新的节点时，利用增量平滑和贝叶斯树（iSAM2）¹⁹的映射，对因子图进行优化。生成因子的过程在以下章节说明。

B. IMU预积分因子

IMU测量的角速度和加速度用方程描述：

$$ \begin{align} \hat{\boldsymbol{\omega}}_t&=\boldsymbol{\omega}_t+\mathbf{b}_t^{\boldsymbol{\omega}}+\mathbf{n}_t^{\boldsymbol{\omega}} \\ \hat{\mathbf{a}}_t&=\mathbf{R}_t^{\mathbf{BW}}(\mathbf{a}_t-\mathbf{g})+\mathbf{b}_t^{\mathbf{a}}+\mathbf{n}_t^{\mathbf{a}} \end{align} $$

其中$\hat{\boldsymbol{\omega}_t}$和$\hat{\mathbf{a}_t}$为原始IMU在$\mathbf{B}$框架$t$时刻的测量值。$\hat{\boldsymbol{\omega}_t}$和$\hat{\mathbf{a}_t}$受到缓慢变大的偏差$\mathbf{b}_t$和白噪声$\mathbf{n}_t$影响。$\mathbf{R}_t^{\mathbf{BW}}$为从$\mathbf{W}$变换到$\mathbf{B}$的变换矩阵。$\mathbf{g}$为$\mathbf{W}$中的重力加速度常数向量

我们现在可以使用从IMU测量的值推算机器人的移动。机器人在时刻$t+\Delta t$的速度、位置和旋转通过以下计算：

$$ \begin{align} \mathbf{v}_{t+\Delta t}&=\mathbf{v}_t+\mathbf{g}\Delta t+\mathbf{R}_t(\hat{\mathbf{a}}_t-\mathbf{b}_t^{\mathbf{a}}-\mathbf{n}_t^{\mathbf{a}})\Delta t\\ \mathbf{p}_{t+\Delta t}&=\mathbf{p}_t+\mathbf{v}_t\Delta t+\frac{1}{2}\mathbf{g}t^2+ \frac{1}{2}\mathbf{R}_t(\hat{\mathbf{a}}_t-\mathbf{b}_t^{\mathbf{a}}-\mathbf{n}_t^{\mathbf{a}})\Delta t^2\\ \mathbf{R}_{t+\Delta t}&=\mathbf{R}_t \space\mathbf{exp}\left((\hat{\boldsymbol{\omega}}_t-\mathbf{b}_t^{\boldsymbol{\omega}}-\mathbf{n}_t^{\boldsymbol{\omega}})\Delta t\right) \end{align} $$

其中$\mathbf{R}_t=\mathbf{R}_t^{\mathbf{WB}}={\mathbf{R}_t^{\mathbf{WB}}}^{\mathsf{T}}$。这里假设$\mathbf{B}$的角速度和加速度在上述积分中保持不变。

然后我们应用²⁰中提出的IMU预积分方法来获得两个时间段之间的相对运动。时刻$i$到$j$的预积分测量量$\Delta \mathbf{v}_{ij}$、$\Delta \mathbf{p}_{ij}$和$\Delta \mathbf{R}_{ij}$通过以下方法计算：

$$ \begin{align} \Delta \mathbf{v}_{ij}&=\mathbf{R}_i^{\mathsf{T}}(\mathbf{v}_j-\mathbf{v}_i-\mathbf{g}\Delta t_{ij}) \\ \Delta \mathbf{p}_{ij}&=\mathbf{R}_i^{\mathsf{T}}(\mathbf{p}_j-\mathbf{p}_i-\mathbf{v}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2) \\ \Delta \mathbf{R}_{ij}&= \mathbf{R}_i^{\mathsf{T}}\mathbf{R}_j \end{align} $$

对于旋转矩阵来说，$\mathbf{R}_i^{\mathsf{T}}=\mathbf{R}_i^{-1}$。方程的推导在另外的地方²⁰。除去它的效率，应用IMU预积分也自然给我们提供了一种因子图的约束——IMU预积分因子。在图中，IMU的偏差与激光雷达的里程计因子一起被联合优化。

C. 激光雷达里程计因子

当新的激光雷达扫描到来，我们首先执行特征提取。通过评估本地区域点的粗糙度提取边缘（Edge）和平面（Planar）特征。粗糙度大的点归为角特征。同样的，平面特征点粗糙度较小。定义在激光雷达$i$时刻提取的边缘和平面特征分别为$\text{F}^e_i$和$\text{F}^p_i$。$i$时刻提取的所有特征组成激光雷达帧$\mathbb{F}_i$，其中$\mathbb{F}_i=\{\text{F}_i^e, \text{F}_i^p\}$。定义$\mathbf{B}$中的激光雷达帧为$\mathbb{F}$。更详细的特征提取过程在¹或者如果有使用到距离图像⁷中找到。

使用每一个激光雷达帧来计算并向图中添加因子在计算上是难以实现的，因此我们采用了关键帧选择的概念，这在视觉SLAM领域被广泛使用。使用一个简单而有效的启发式方法，当机器人位置状态相对于之前的状态$\mathbf{x}_i$发生变换并且超过用户定义的阈值时，我们选择一帧激光雷达$\mathbb{F}_{i+1}$作为关键帧。新保存的关键帧，$\mathbb{F}_{i+1}$，和新的机器人在因子图中的状态节点$\mathbf{x}_{i+1}$进行关联。关键帧之间的雷达数据被丢弃。通过这种方式添加关键帧不仅实现了地图密度和内存消耗之间的平衡，而且有助于保持一个相对稀疏的因子图，这适合于实时非线性优化。在我们的工作中，添加关键帧的距离和旋转阈值为1m和10°。

假设我们希望添加新的状态节点$\mathbf{x}_{i+1}$到因子图。和当前状态相关的激光雷达关键帧为$\mathbb{F}_{i+1}$。激光雷达里程计因子生成步骤描述如下：

1. 点云地图子关键帧

我们使用了一个滑动窗口的方法来创建一个包含固定数量的最近激光雷达扫描的点云地图。我们提取最近的$n$帧最近关键帧，又叫子关键帧，用来估计，而不是优化两个连续激光雷达扫描之间的转换。子关键帧集合$\{\mathbb{F}_{i-n},\dots,\mathbb{F}_i\}$然后使用变换$\{\mathbf{T}_{i-n},\dots,\mathbf{T}_i\}$关联到它们变换到框架$\mathbf{W}$里面。变换好的子关键帧合并到点云地图$\mathbf{M}_i$中。由于我们在之前的特征提取步骤中提取了两种特征，$\mathbf{M}_i$由两种点云地图构成，代表边缘特征的$\mathbf{M}_i^e$和代表平面特征的$\mathbf{M}_i^p$。激光雷达帧和点云地图关系如下：

$$ \begin{align} &\mathbf{M}_i=\{\mathbf{M}_i^e,\mathbf{M}_i^p\}\\ &\mathsf{其中:}\space\mathbf{M}_i^e=\mathbf{'F}_i^e\cup\mathbf{'F}_{i-1}^e\cup\ldots\cup\mathbf{'F}_{i-n}^e\\ &\qquad \space \space\mathbf{M}_i^p=\mathbf{'F}_i^p\cup\mathbf{'F}_{i-1}^p\cup\ldots\cup\mathbf{'F}_{i-n}^p \end{align} $$

$\mathbf{'F}_i^e$和$\mathbf{'F}_i^p$为$\mathbf{W}$框架下变换过的边缘和平面特征。然后对$\mathbf{M}_i^e$和$\mathbf{M}_i^p$进行下采样，以消除落在同一体素单元中的重复特征。在本论文中，$n$选定为25。下采样分辨率对应$\mathbf{M}_i^e$和$\mathbf{M}_i^p$分别为0.2m和0.4m。

2. 扫描匹配

我们使用新得到的激光雷达帧$\mathbb{F}_{i+1}$，也就是$\{\text{F}_{i+1}^e, \text{F}_{i+1}^p\}$，通过扫描-匹配匹配到$\mathbf{M}_i$。不同的扫描-匹配方法，例如³和⁴，可用于此目的。我们选择使用¹中的方法由于它在不同的环境下计算效率和鲁棒性。

我们首先把$\{\text{F}_{i+1}^e, \text{F}_{i+1}^p\}$从$\mathbf{B}$转换到$\mathbf{W}$得到$\{\mathbf{'F}_{i+1}^e,\mathbf{'F}_{i+1}^p\}$。这次初始变换从机器人运动预测中得到，$\tilde{\mathbf{T}}_{i+1}$，从IMU。对于每个$\mathbf{'F}_{i+1}^e$或$\mathbf{'F}_{i+1}^p$中的特征，我们找到它的边缘或平面碎片和$\mathbf{M}_i^e$或$\mathbf{M}_i^p$的关系。为了简洁起见，这里省略了寻找这些对应关系的详细程序，但在¹中进行了详尽的描述。

3. 相对变换

一个特征与它的边缘或平面对应的距离可以用以下公式来计算：

$$ \mathbf{d}_{e_k}=\frac{\left|(\mathbf{p}_{i+1,k}^e-\mathbf{p}_{i,u}^e)\times(\mathbf{p}_{i+1,k}^e-\mathbf{p}_{i,v}^e)\right|}{\left|\mathbf{p}_{i,u}^e-\mathbf{p}_{i,v}^e\right|} $$ $$ \mathbf{d}_{p_k}=\frac{ \begin{vmatrix} (\mathbf{p}_{i+1,k}^p-\mathbf{p}_{i,u}^p)\\ (\mathbf{p}_{i,u}^p-\mathbf{p}_{i,v}^p)\times(\mathbf{p}_{i,u}^p-\mathbf{p}_{i,w}^p) \end{vmatrix}} {\begin{vmatrix} (\mathbf{p}_{i,u}^p-\mathbf{p}_{i,v}^p)\times(\mathbf{p}_{i,u}^p-\mathbf{p}_{i,w}^p) \end{vmatrix}} $$

其中，$k$、$u$、$v$和$w$是其相应集合中的特征指数。在$\mathbf{'F}_{i+1}^e$、$\mathbf{p}_{i,u}^e$和$\mathbf{p}_{i,v}^e$中的边缘特征$\mathbf{p}_{i+1,k}^e$是构成$\mathbf{M}_i^e$中相应边线的点。在$\mathbf{'F}_{i+1}^p$、$\mathbf{p}_{i,u}^p$、$\mathbf{p}_{i,v}^p$和$\mathbf{p}_{i,w}^p$的平面特征$\mathbf{p}_{i+1,k}^p$是构成$\mathbf{M}_i^p$中相应的平面的碎片。然后使用高斯-牛顿方法通过最小化来求解最佳的变换：

$$ \sideset{}{}\min_{\mathbf{T}_{i+1}}\left\{ \sum_{\mathbf{p}_{i+1,k}^e\in \mathbf{'F}_{i+1}^e} \mathbf{d}_{e_k}+ \sum_{\mathbf{p}_{i+1,k}^p\in \mathbf{'F}_{i+1}^p} \mathbf{d}_{p_k}+ \right\} $$

最后，我们可以得到从$\mathbf{x}_i$到$\mathbf{x}_{i+1}$的相对变换$\Delta \mathbf{T}_{i,i+1}$，由激光雷达里程计因子链接两个位置：

$$ \Delta \mathbf{T}_{i,i+1}=\mathbf{T}_i^{\mathsf{T}}\mathbf{T}_{i+1} $$

我们注意到，获得$\Delta \mathbf{T}_{i,i+1}$的另一种方法是将子关键帧转换到$\mathbf{x}_i$框架的框架。换句话说，我们将$\mathbb{F}_i$与$\mathbf{x}_i$的框架中所代表的点云地图相匹配。在这种方式中真实的相对变换$\Delta \mathbf{T}_{i,i+1}$可以直接获得。由于变换过的特征$\mathbf{'F}_i^e$和$\mathbf{'F}_i^p$可以多次重复使用，我们选择使用在第III-C.1章中描述的方法。

D. GPS因子

尽管我们可以通过仅利用IMU预积分和激光雷达里程计因子来获得可靠的状态估计和建图，但在长时间的导航任务中，系统仍然受到漂移的影响。为了解决这个问题，我们可以引入提供绝对测量的传感器来消除漂移。这样的传感器包括高度计、罗盘和GPS。为了说明问题，我们在此讨论GPS，因为它在现实世界的导航系统中被广泛使用。

当我们收到GPS测量数据时，我们首先使用²¹中提出的方法将其转换为本地直角坐标框架。在因子图上增加一个新的节点后，我们就将一个新的GPS因子与这个节点联系起来。如果GPS信号没有与激光雷达框架进行硬件同步，我们就根据激光雷达框架的时间戳在GPS测量值之间进行线性插值。

我们注意到，在有GPS接收的情况下，不断添加GPS因子是没有必要的，因为激光雷达惯性里程计的漂移增长非常缓慢。在实践中，我们只在估计的位置协方差大于接收到的GPS位置协方差时才添加GPS因子。

E. 闭环因子

由于对因子图的利用，与LOAM和LIOM不同，环路闭合也可以无缝地纳入拟议的系统中。为了说明问题，我们描述并实现了一个简单但有效的基于欧氏距离的闭环检测方法。我们还注意到，我们提出的框架与其他的环路闭环检测方法是兼容的，例如，²²和²³，它们生成了一个点云描述符并将其用于地方识别。

当一个新的状态$\mathbf{x}_{i+1}$添加到因子图中时，我们首先搜索图找到之前状态中在欧氏距离上和$\mathbf{x}_{i+1}$接近的状态。如在框架图中描述的，例如，$\mathbf{x}_{3}$为其中返回的一个备选项。然后我们尝试使用扫描-匹配把$\mathbb{F}_{i+1}$匹配到子关键帧$\{\mathbb{F}_{3-m},\ldots,\mathbb{F},\ldots,\mathbb{F}_{3+m}\}$。注意$\mathbb{F}_{i+1}$和之前的子关键帧在进行扫描-匹配前需要先变换到$\mathbf{W}$里面。我们得到相对变换$\Delta \mathbf{T}_{3,i+1}$并把它作为闭环因子加入到因子图中去。在本论文中，我们选择$m$为12，从新的状态$\mathbf{x}_{i+1}$搜索闭环的距离为15m。

在实践中，我们发现当GPS为仅有的可用的绝对传感器时，添加闭环因子能够有效的纠正机器人高度上的漂移。这是因为GPS的高程测量非常不准确——在缺乏闭环的测试中高度误差接近100m。

参考文献

[24]: M. Quigley, K. Conley, B. Gerkey, J. Faust, T. Foote, J. Leibs, R. Wheeler, and A.Y. Ng, “ROS: An Open-source Robot Operating System,” IEEE ICRA Workshop on Open Source Software, 2009.

[25]: T. Qin, P. Li, and S. Shen, “Vins-mono: A Robust and Versatile Monocular Visual-Inertial State Estimator,” IEEE Transactions on Robotics, vol. 34(4): 1004-1020, 2018.