原文链接：gtsam.pdf

概述

因子图是很适合解决复杂估计问题的图形化模型，例如SLAM或者运动结构恢复（Structure from Motion，SFM）。你可能熟悉其他常用的图形模型，是有向无环图的贝叶斯网络。因子图，是一个由与变量相连的因子组成的二分图，这些变量代表估计问题中的未知随机变量，而因子则代表这些变量的概率约束，这些约束来自测量或先验知识。在下面的章节中，我将用机器人学和视觉学的例子来说明这一点。

GTSAM工具箱（GTSAM表示“Georgia Tech Smoothing and Mapping”）为BSD协议的基于因子图的C++库，由我在Georgia Institute of Technology自己、学生们和同事们。它为SLAM和SFM问题提供了最先进的解决方案，但也可用于建模和解决更简单和更复杂的估计问题。它还提供了一个MATLAB界面，可以进行快速的原型开发、可视化和用户互动。

GTSAM利用稀疏性来提高计算效率。通常情况下，测量只提供少数变量之间的关系信息，因此产生的因子图将是稀疏的连接。GTSAM中实施的算法利用了这一点，以减少计算的复杂性。即使当图太密集而无法用直接方法有效处理时，GTSAM提供的迭代方法也是相当有效的。

你可以在以下网址下载最新版本的GTSAM：http://tinyurl.com/gtsam

1 因子图

让我们从一页的因素图入门开始

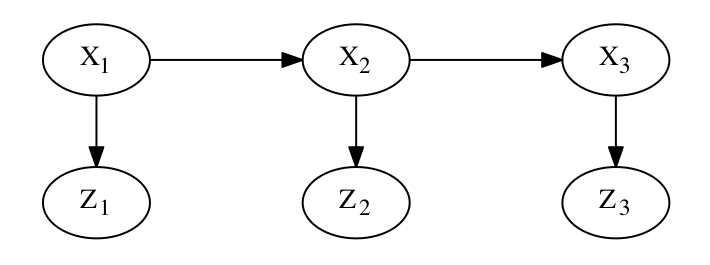
图1，一个HMM，在三个时间步长上展开，表示贝叶斯网络

图1展示了三个时间步长上面的一个隐马尔可夫模型的贝叶斯网络表示。在贝叶斯网中，每个节点都与条件密度有关：顶部马尔可夫链编码了先验$P(X_1)$和过渡概率$P(X_2|X_1)$和$P(X_3 |X_2)$，而测量值$Z_t$只取决于状态$X_t$，由条件密度$P(Z_t|X_t)$建模。给定已知的测量参数$z_1$，$z_2$和$z_3$我们感兴趣的是使得后验概率$P(X_1,X_2,X_3|Z_1=z_1,Z_2=z_2,Z_3=z_3)$最大的隐藏状态序列$(X_1,X_2,X_3)$。由于测量值$Z_1$，$Z_2$和$Z_3$已知，后验与六个因子的乘积成正比，其中三个因子来自马尔科夫链，三个似然因子定义为$L(X_t;z)\propto P(Z_t=z|X_t)$：

$$ P(X_1,X_2,X_3|Z_1,Z_2,Z_3)\propto P(X_1)P(X_2|X_1)P(X_3|X_2)L(X_1;z_1)L(X_2;z_2)L(X_3,z_3) $$

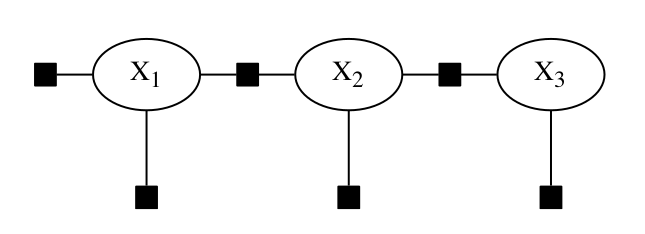
图2：一个具有观察测量值的HMM，随着时间的推移而展开，表示为一个因子图

这促使我们采用不同的图形模型，即因子图，其中我们只表示未知变量$X_1$、$X_2$和$X_3$，与编码它们的概率信息的因子相连，如图2所示。为了进行最大后验（MAP，maximum a-posteriori）推理，我们将最大限度地提高乘积

$$ f(X_1,X_2,X_3)=\prod f_i(\mathcal{X}_i) $$

即因子图的值。因子图编码的连接从图上看应该很清楚，对于每个因子$f_i$，取决于变量子集$\mathcal{X}_i$。在下面的例子中，我们用因子图来对机器人学中更加复杂的最大后验推理问题进行建模。

2 对机器人运动建模

完整的代码在 https://github.com/borglab/gtsam/blob/develop/examples/OdometryExample.cpp

2.1 使用因子图建模

在深入SLAM例子之前，让我们先考虑机器人运动中简单问题的建模。这可以用连续马尔可夫链来完成，并为GTSAM提供一个简单的介绍。

图3：机器人定位因子图

简单例子的因子图如图3所示。这里有三个变量$x_1$，$x_2$和$x_3$代表机器人随时间位置的变化，在图中由开圆的变量节点呈现。在该例子中，我们在第一个姿态$x_1$上有一个一元因子$f_0(x_1)$，编码我们关于$x_1$的先验知识，还有两个二元因子将连续的姿态联系起来，分别是$f_1(x_1 , x_2 ; o_1 )$和$f_2 (x_2 , x_3 ; o_2 )$，其中$o_1$和$o_2$代表里程测量值。

2.2 创建因子图

下面的C++代码，包含在GTSAM中作为例子，创建了图3中的因子图：

 1// 创建空的非线性因子图
 2NonlinearFactorGraph graph;
 3
 4//在位置x_1位置添加高斯先验
 5Pose2 priorMean(0.0, 0.0, 0.0);
 6noiseModel::Diagonal::shared_ptr priorNoise =
 7    noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1));
 8graph.addPrior(1, priorMean, priorNoise);
 9
10// 添加两个里程因子
11Pose2 odometry(2.0, 0.0, 0.0);
12noiseModel::Diagonal::shared_ptr odometryNoise =
13    noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
14graph.add(BetweenFactor<Pose2>(1, 2, odometry, odometryNoise));
15graph.add(BetweenFactor<Pose2>(2, 3, odometry, odometryNoise));
16graph.print("\nFactor Graph:\n");
清单1：摘自examples/OdometryExample.cpp

上面，第2行创建了一个空的因子图。然后我们在第5-8行添加因子$f_0(x_1)$作为一个在slam子目录下提供的模板类**PriorFactor<T>的实例，其中T=Pose2。它的构造函数需要一个变量Key（在这里是1），一个在第5行创建的Pose2均值类型，以及一个用于先验密度的噪声模型。我们通过在第7行中指定三个标准差来提供一个对角线高斯类型noiseModel::Diagonal，分别是机器人位置上的30厘米和机器人方向上的0.1弧度。需要注意的是Sigmas**构造函数返回共享指针，预计通常情况下，相同的噪声模型被用于许多不同的因素。

相同的，里程计测量值在第11行中用**Pose2指定，有着稍微不同的噪声模型，定义在第12-13行。然后我们在第14-15行把两个因子$f_1(x_1,x_2;o_1)$和$f_2(x_2,x_3;o_2)$作为另外一个模板类BetweenFactor<T>的实例添加进去，其中T=Pose2**。

当我们运行例子（命令行执行make OdometryExample），它会打印因子图如下：

Factor Graph:
size: 3

Factor 0: PriorFactor on 1
  prior mean:  (0, 0, 0)
  noise model: diagonal sigmas[0.3; 0.3; 0.1];

Factor 1: BetweenFactor(1,2)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas[0.2; 0.2; 0.1];

Factor 2: BetweenFactor(2,3)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas[0.2; 0.2; 0.1];

2.3 因子图相对（versus）值

在这一点上，强调GTSAM的两个重要的设计理念是很有意义的：

  1. 因子图及其在代码中的体现指定了机器人整个轨迹$X\triangleq\{x_1 , x_2 , x_3\}$的联合概率分布$P(X|Z)$，而不仅仅是最后的姿势。这种平滑的世界观给了GTSAM一个名字：“平滑和映射”。在本文的后面，我们将讨论如何使用GTSAM来做滤波（你经常不想做）或增量推导（我们一直在做）。
  2. GTSAM中的因子图只是对概率密度$P(X|Z)$的规范，相应的**FactorGraph类和它的派生类并不包含“解决方案”。相反，有一个单独的类型Values**，用来指定（本例中）$x_1$、$x_2$和$x_3$的特定值，然后可以用来评估与特定值相关的概率（或者，更常见的，误差）。

后面一点是一开始使用GTSAM的人经常迷惑的。请记住，在设计GTSAM时，我们采取了对应于数学对象的类的功能方法，这些对象通常是不可变的。你应该把因子图看作是一个应用于数值的函数——正如符号$f (X) \propto (X|Z)$所暗示的那样——而不是看作一个要修改的对象。

2.4 GTSAM中的非线性优化

下面的清单创建了一个**Values**类的实例，并且使用它作为初值来寻找航迹$X$的最大后验值

1// 创建（故意不准确的）初步估计
2Values initial;
3initial.insert(1, Pose2(0.5, 0.0, 0.2));
4initial.insert(2, Pose2(2.3, 0.1, -0.2));
5initial.insert(3, Pose2(4.1, 0.1, 0.1));
6
7// 使用Levenberg-Marquardt优化法进行优化
8Values result = LevenbergMarquardtOptimizer(graph, initial).optimize();
9result.print("Initial Estimate");
清单2：摘自examples/OdometryExample.cpp
清单2中的第2-5行创建了初始估计值，在第8行我们创建了一个非线性Levenberg-Marquardt风格的优化器，并使用默认参数设置调用***`optimize`***。GTSAM需要执行非线性优化的原因是里程因子$f_1(x_1,x_2;o_1)$和$f_2(x_2,x_3;o_2)$由于它们参与机器人的旋转，都是非线性的。这也解释了为什么在清单1中创建的因子图的类型为***`NonlinearFactorGraph`***。这个优化类线性化这个图，可能乘上时间，来减小因子指定的非线性方差。

例子的输出如下：

Initial Estimate
Values with 3 values:
Value 1: (gtsam::Pose2)
(7.46978309e-16, -5.34409095e-16, -1.78381861e-16)

Value 2: (gtsam::Pose2)
(2, -1.09236636e-15, -2.48671177e-16)

Value 3: (gtsam::Pose2)
(4, -1.70076056e-15, -2.50943862e-16)

可以看出，在非常小的容忍度下，地面真实的解$x_1=(0,0,0)$，$x_2=(2,0,0)$和$x_3=(4,0,0)$被恢复了

2.5 完全后验推断

边缘分布：

$$ F_X(x)=F(x,+\infty)=\int_{-\infty}^xdx\int_{-\infty}^{+\infty}f(x,y)dy $$ $$ f_X(x)=\frac{d}{dx}F_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy $$

在纳入所有测量值$Z$的信息后，GTSAM也可以用来计算每个姿势的协方差矩阵。认识到因子图编码了后验密度$P(X|Z)$，每个姿势$x$的平均数$\mu$连同协方差$\Sigma$近似于边缘后验密度（marginal posterior density）$P(x|Z)$。请注意，这只是一个近似值，因为即使在这种简单的情况下，测距因子的参数实际上也是非线性的，而GTSAM只是计算了一个真正的基础后验的高斯近似值。

以下C++代码能够恢复边缘后验：

1// 查询边缘
2cout.precision(2);
3Marginals marginals(graph, result);
4cout << "x1 covariance: \n" << marginals.marginalCovariance(1) << endl;
5cout << "x2 covariance: \n" << marginals.marginalCovariance(2) << endl;
6cout << "x3 covariance: \n" << marginals.marginalCovariance(3) << endl;
清单3：摘自examples/OdometryExample.cpp

例子运行结果为：

x1 covariance:
   0.09 3.2e-33 2.8e-33
3.2e-33    0.09 2.6e-17
2.8e-33 2.6e-17    0.01
x2 covariance:
   0.13 1.2e-18 6.1e-19
1.2e-18    0.17    0.02
6.1e-19    0.02    0.02
x3 covariance:
   0.17 8.6e-18 2.7e-18
8.6e-18    0.37    0.06
2.7e-18    0.06    0.03

我们可以看到

我们可以看到的是$x_1$的边缘协方差$P(x_1,Z)$只是简单的基于$x_1$的先验知识，但随着机器人的移动，所有维度的不确定性都在无限制地增长，姿势的$y$和$\theta$成分变得（正）相关。

在解释这些数字时要注意的一个重要事实是协方差矩阵是以相对坐标而不是绝对坐标给出的。这是因为在内部GTSAM优化了相对于线性化点的变化，就像所有的非线性优化库一样。

3 机器人定位

3.1 单一的测量因素

在这一节中，我们将测量结果添加到因子图中，这将帮助我们在一段时间内实际定位机器人。这个例子也可以作为创建新因素类型的教程。

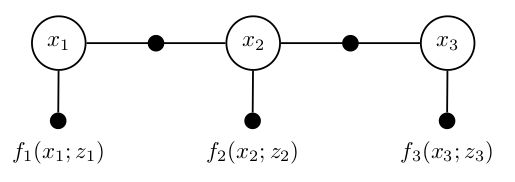
图4：机器人定位因子图在每个步骤使用单一测量因子

特别的，我们使用单一测量因子来处理外部测量。第2节中的例子在真实的机器人上不是很有用，因为它只包含与测距仪测量相对应的因素。这些都是不完善的，会导致最后的机器人姿态的不确定性迅速累积，至少在没有任何外部测量的情况下是如此（见第2.5节）。图4展示了一个新的因子图，其中先验$f_0(x_1)$被省略了同时我们添加了三个单一因子$f_1(x_1:z_1)$，$f_2(x_2:z_2)$和$f_3(x_3:z_3)$，对每个定位测量值$z_t$分别都有一个。这种单一因子适用于只取决于当前机器人姿势的测量值$z_t$，例如，GPS读数、预先存在的地图中激光测距仪的相关性，或者确实存在或没有天花板上的灯。

3.2 定义自定义因子

在GTSAM里，你可以通过从內建的类**NoiseModelFactor1<T>**派生新类，创建自定义单一因子。该模板类实现了一个与高斯噪声模型的测量似然性相对应的单因素

$$ L(q;m)=\exp\left\{-\frac{1}{2}\|h(q)-m\|_\Sigma^2\right\}\triangleq f(q) $$

其中$m$为测量值，$q$为未知变量，$h(q)$为一个（可能非线性）测量函数，$\Sigma$为噪声协方差。注意上面的$m$为已知，而可能性$L(q; m)$将只作为$q$的函数被评估，这就解释了为什么它是一个单一因子$f(q)$。鉴于测量结果，可能或不可能的总是未知变量$q$。

**注意：**许多人把这个问题弄反了，常常被条件密度符号$P(m|q)$所误导。事实上，可能性$L(q; m)$被定义为与$P(m|q)$成比例的$q$的任何函数。

清单4展示了一个关于如何定义自定义因子类**UnaryFactor**的例子，它实现了一个“类似GPS”的测量可能性：

 1class UnaryFactor : public NoiseModelFactor1<Pose2>
 2{
 3    double mx_, my_;        ///< X和Y测量值
 4public:
 5    UnaryFactor(Key j, double x, double y, const SharedNoiseModel &model) :
 6            NoiseModelFactor1<Pose2>(model, j), mx_(x), my_(y) {}
 7
 8    Vector evaluateError(const Pose2 &q,
 9                         boost::optional<Matrix &> H) const override
10    {
11        const Rot2 &R = q.rotation();
12        if (H) {
13            (*H) = (gtsam::Matrix(2, 3) <<
14                    R.c(), -R.s(), 0.0,
15                    R.s(), R.c(), 0.0).finished();
16        }
17        return (Vector(2) << q.x() -mx_, q.y() - my_).finished();
18    }
19};
清单4：摘自examples/LocalizationExample.cpp

在第1行定义的派生类中，我们用模板变量**Pose2来表示变量$q$的类型，而测量结果被存储为实例变量mx_和my_，定义在第3行。第5-6行的构造函数只是将变量键j和噪声模型传递给父类，并存储提供的测量值。每个因子类必须实现的最重要的函数是evaluateError**，它应该返回

$$ E(q)\triangleq h(q)-m $$

在12行已经完成。重要的是，因为我们想把这个因素用于非线性优化（详见Dellaert和Kaess 2006），只要提供可选的参数$H$，即一个矩阵参考，函数就应该把$h(q)$的雅可比系数分配给它，在提供的$q$值上进行评估。在这种情况下，二维函数$h$的雅可比，它只是返回机器人的位置

$$ h(q)=\begin{bmatrix} q_x\\ q_y \end{bmatrix} $$

相对于三维姿势$q = (q_x , q_y , q_\theta)$，产生以下切线空间的简单$2\times3$矩阵，与旋转矩阵相同：

$$ H=\begin{bmatrix} \cos(q_\theta) & -\sin(q_\theta) & 0 \\ \sin(q_\theta) & \cos(q_\theta) & 0 \\ \end{bmatrix} $$

3.3 使用自定义因子

下面的C++代码片段说明了如何创建和添加自定义因子到一个因子图：

1// 添加单一测量因子，比如GPS，在所有的三个位置
2auto unaryNoise = noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1));	// 10cm 标准差 on x,y
3graph.add(boost::make_shared<UnaryFactor>(1, 0.0, 0.0, unaryNoise));
4graph.add(boost::make_shared<UnaryFactor>(2, 2.0, 0.0, unaryNoise));
5graph.add(boost::make_shared<UnaryFactor>(3, 4.0, 0.0, unaryNoise));
清单5：摘自examples/LocalizationExample.cpp

在清单5中，我们在第2行创建噪声模型，对于测量量$m_x$和$m_y$指定了两个标准差。在第3-5行创建了三个新的**UnaryFactor**实例，添加到图中。GTSAM使用共享指针指向因子图中的因子。我们得到图4中的因子图。

3.4 完全后验推断

三个GPS因子足以完全约束所有的未知姿态，并将它们与一个“全局”参考框架联系起来，包括三个未知方向。如果不是这样，GTSAM就会以奇异矩阵的方式退出。边缘可以完全按照第2.5节中的方法恢复，现在解和边缘协方差如下：

Initial Estimate
Values with 3 values:
Value 1: (gtsam::Pose2)
(1.42811204e-12, -3.93007852e-12, -4.27083461e-12)

Value 2: (gtsam::Pose2)
(2, 6.60078282e-12, 1.92677797e-13)

Value 3: (gtsam::Pose2)
(4, -2.23396394e-12, 1.90220289e-13)

x1 covariance:
  0.0076 -4.6e-15  1.3e-14
-4.6e-15   0.0081  -0.0015
 1.3e-14  -0.0015   0.0045
x2 covariance:
  0.0071  8.5e-16 -1.3e-14
 8.5e-16   0.0077  -0.0014
-1.3e-14  -0.0014   0.0072
x3 covariance:
 0.0083 3.8e-15 1.1e-14
3.8e-15  0.0092  0.0026
1.1e-14  0.0026   0.017

NOTE: Python绘制结果代码如下：

 1import filterpy.stats as stats
 2import matplotlib.pyplot as plt
 3import numpy as np
 4import math
 5
 6
 7# 绘制5 Sigma椭圆，每个乘以sqrt(5)
 8def plot_odometry_result():
 9    fig = plt.figure()
10    plt.title("Odometry")
11    x = np.array([7.46978309e-16, -5.34409095e-16])
12    P = np.array([[0.09, 3.2e-33],
13                  [3.2e-33, 0.09]])
14    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
15    x = np.array([2, -1.09236636e-15])
16    P = np.array([[0.13, 1.2e-18],
17                  [1.2e-18, 0.17]])
18    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
19    x = np.array([4, -1.70076056e-15])
20    P = np.array([[0.17, 8.6e-18],
21                  [2.7e-18, 0.37]])
22    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
23    plt.xlabel('x')
24    plt.ylabel('y')
25    plt.axis('equal')
26
27
28def plot_localization_result():
29    fig = plt.figure()
30    plt.title("Localization")
31    x = np.array([1.42811204e-12, -3.93007852e-12])
32    P = np.array([[0.0076, -4.6e-15],
33                  [-4.6e-15, 0.0081]])
34    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
35    x = np.array([2, 6.60078282e-12])
36    P = np.array([[0.0071, 8.5e-16],
37                  [8.5e-16, 0.0077]])
38    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
39    x = np.array([4, -2.23396394e-12])
40    P = np.array([[0.0083, 3.8e-15],
41                  [3.8e-15, 0.0092]])
42    stats.plot_covariance(x, P * math.sqrt(5), facecolor='b', alpha=0.6)
43    plt.xlabel('x')
44    plt.ylabel('y')
45    plt.axis('equal')
46
47
48if __name__ == "__main__":
49    plot_odometry_result()
50    plot_localization_result()
51    plt.show()

将2这与第2.5节中的协方差矩阵相比较，我们可以看到，随着测量不确定性的积累，不确定性不再无限制的增长。相反，“GPS “均值或多或少地约束了姿势，正如预期的那样：

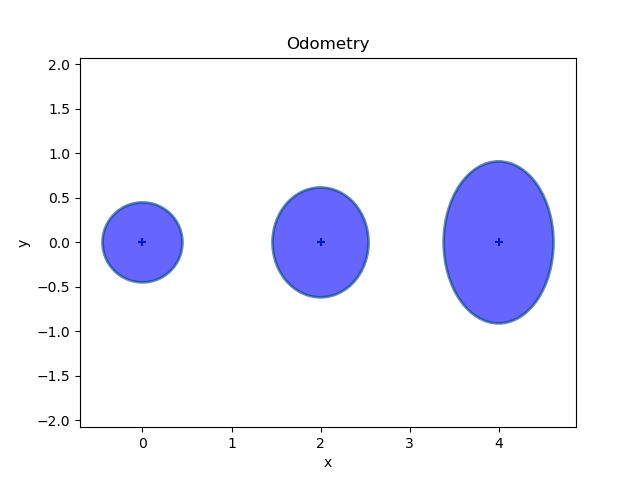
(a)里程计边缘

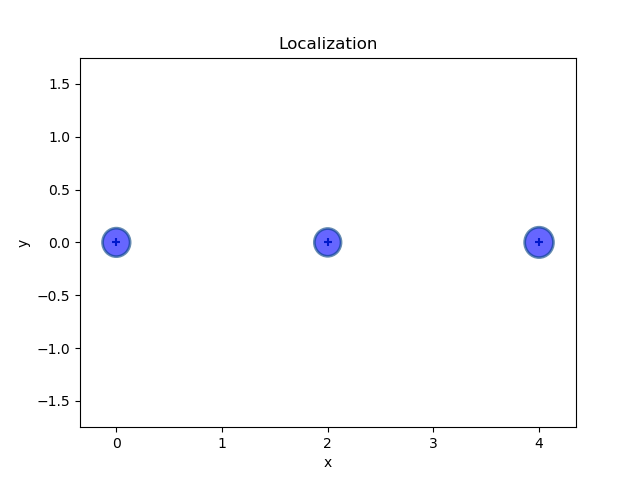
(b)定位边缘

图5：比较里程计因子图（图3）和定位因子图（图4）边缘结果

当我们用图形来看待这个问题时，会有很大的帮助，如图5，我把位置上的边际显示为5西格玛协方差椭圆，包含了所有概率质量的99.9996%。对于运动学边际，从图中可以立即看出：（1）姿势的不确定性不断增加，以及（2）角度运动学的不确定性转化为y的不确定性不断增加。相比之下，定位边际受到单因素的制约，都要小得多。此外，虽然不太明显，但中间姿态的不确定性实际上更小，因为它受到来自两边的里程数的制约。