节点话题图
LIO-SAM图优化中角点优化中PCA
介绍
看LIO-SAM代码的时候,看到角点优化函数里面通过协方差特征值判断是否为角点,代码如下
kdtreeCornerFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);
cv::Mat matA1(3, 3, CV_32F, cv::Scalar::all(0));
cv::Mat matD1(1, 3, CV_32F, cv::Scalar::all(0));
cv::Mat matV1(3, 3, CV_32F, cv::Scalar::all(0));
// 最后一个点距离<1.0意味着所有的距离都小于1m
if (pointSearchSqDis[4] < 1.0) {
float cx = 0, cy = 0, cz = 0;
for (int j = 0; j < 5; j++) {
cx += laserCloudCornerFromMapDS->points[pointSearchInd[j]].x;
cy += laserCloudCornerFromMapDS->points[pointSearchInd[j]].y;
cz += laserCloudCornerFromMapDS->points[pointSearchInd[j]].z;
}
// 5个点取均值
cx /= 5;
cy /= 5;
cz /= 5;
float a11 = 0, a12 = 0, a13 = 0, a22 = 0, a23 = 0, a33 = 0;
for (int j = 0; j < 5; j++) {
float ax = laserCloudCornerFromMapDS->points[pointSearchInd[j]].x - cx;
float ay = laserCloudCornerFromMapDS->points[pointSearchInd[j]].y - cy;
float az = laserCloudCornerFromMapDS->points[pointSearchInd[j]].z - cz;
a11 += ax * ax;
a12 += ax * ay;
a13 += ax * az;
a22 += ay * ay;
a23 += ay * az;
a33 += az * az;
}
// 下标相同的为方差
// 下标不同的为协方差
a11 /= 5;
a12 /= 5;
a13 /= 5;
a22 /= 5;
a23 /= 5;
a33 /= 5;
// 协方差矩阵
matA1.at<float>(0, 0) = a11;
matA1.at<float>(0, 1) = a12;
matA1.at<float>(0, 2) = a13;
matA1.at<float>(1, 0) = a12;
matA1.at<float>(1, 1) = a22;
matA1.at<float>(1, 2) = a23;
matA1.at<float>(2, 0) = a13;
matA1.at<float>(2, 1) = a23;
matA1.at<float>(2, 2) = a33;
// 特征值分解 PCA对角化,得到变换后的坐标系的协方差,
cv::eigen(matA1, matD1, matV1);
// 如果最大的特征值相比次大特征值,大很多,认为构成了线,角点是合格的
if (matD1.at<float>(0, 0) > 3 * matD1.at<float>(0, 1)) {
...通过找资料了解了PCA分析的原理
PCA
大概的意思就是我们对需要处理的数据进行线性变换,使得变换后的数据的协方差为0,使得各个维度变量之间的变量非线性相关,以便单独分析数据的组成。变换后的数据方差越大的维度代表该维度对数据影响较大。
对于LIO-SAM这个问题,基于多线激光雷达的角点,每组角点都在一条折线上(角点提取算法决定)。激光雷达环和平面或者角的交线近似在一个面上,所以有一个维度对数据基本上没有影响。
公式的推导总结
\(X\)为变换前矩阵,\(Y\)为变换后矩阵
\[ Y=PX \]
\(Y\)的协方差为:
\[ \begin{align} D&=\frac{1}{m}YY^T \\ &=\frac{1}{m}(PX)(PX)^T \\ &=\frac{1}{m}PXX^TP^T \\ &=P(\frac{1}{m}XX^T)P^T \\ &=PCP^T \\ \end{align} \]
\(C\)为\(X\)协方差,为对称矩阵
对\(C\)对角化

测试代码
import numpy as np
import matplotlib.pyplot as plt
def dimension3():
"""
用来测试图优化里面的的角点优化
测试结果是折线和直线才能用第一个远大于第二第三个,如果是折面和平面则第一第二个远大于第三个
"""
mat = np.mat([
[1, 1, 0],
[0, 1, 0],
[-1, 1, 0],
[-1, 0, 0],
[-1, -1, 0],
]).T
plt.figure()
ax = plt.subplot(projection='3d')
ax.set_title('origin')
ax.scatter(mat[0], mat[1], mat[2], c='r')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
cov = np.cov(mat)
val, vec = np.linalg.eig(cov)
aft = vec * mat
print(val)
plt.figure()
ax = plt.subplot(projection='3d')
ax.set_title('after')
ax.scatter(aft[0], aft[1], aft[2], c='r')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
print(np.cov(aft))
plt.show()
if __name__ == "__main__":
dimension3()结果:
特征值为:
[0.35 1.25 0. ]
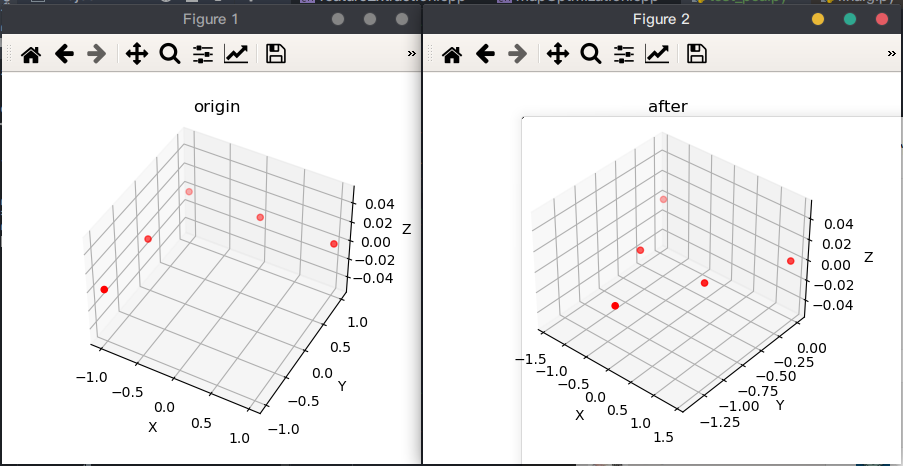
变换后协方差:
[[1.25000000e+00 6.39016933e-17 0.00000000e+00]
[6.39016933e-17 3.50000000e-01 0.00000000e+00]
[0.00000000e+00 0.00000000e+00 0.00000000e+00]]